
Comprendre la profondeur de champ
Quelques calculs d'optique géométrique
La profondeur de champ (que nous noterons DOF par la suite, pour Depth Of Field) est un élément central en photographie, et est souvent mal comprise. Pourtant, c'est un problème simple à comprendre, qui s'appuie sur des notions élémentaires d'optique géométrique et sur le seul théorème de Thalès.
Un petit schéma va nous aider à mieux comprendre le problème de la profondeur de champ:
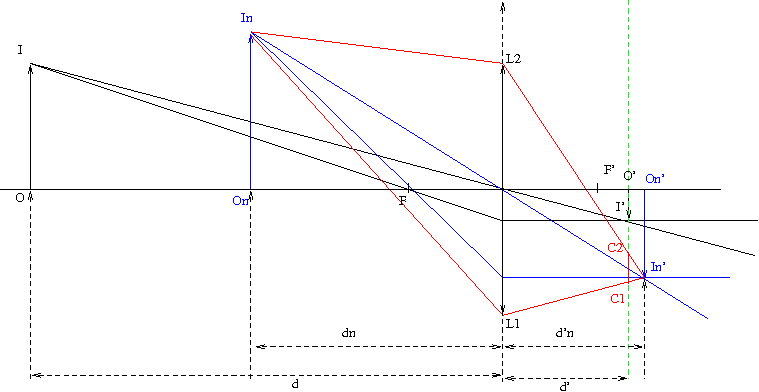
L'objet $OI$ est exactement à la distance de mise au point et son image $O'I'$ est exactement dans le plan du film ou du capteur de l'appareil. $OI$ est à une distance $d$ de l'appareil et l'image $O'I'$ se trouve à la distance $d'$, avec (voir la page fondements de l'optique géométrique): $$d'= d \frac{f}{d - f}$$
Considérons maintenant l'objet $O_nI_n$ (où $n$ signifie
near, proche en anglais). Cet objet est plus proche de
l'appareil que $OI$; il est à une distance
$d_n$ avec $d_n \lt d$.
L'image de $O_nI_n$ est
$O_n'I_n'$ situé à une distance:
$$d_n'= d_n \frac{f}{d_n - f}$$
du centre optique. Cet
objet est situé derrière le plan du film, puisque $d_n' \gt d'$
donc la mise au point sur $O_nI_n$ n'est pas "bonne". En fait,
l'image de chaque point de $O_nI_n$ sur le film, au lieu d'être un
point, est représenté par un cercle, connu sous le nom de cercle
de confusion . C'est la raison pour laquelle les objets qui ne
sont pas exactement à la distance de mise au point apparaissent flous.
Par exemple, le point $I_n$ crée sur le film un cercle dont le diamètre est déterminé par les points $C1$ et $C2$. Ces points sont construits en traçant l'image des deux rayons extrêmes passant par le bord de la lentille et en traçant leur intersection avec le plan du film.
Il est facile de déterminer le diamètre $c$ (distance $C1C2$) du cercle de confusion. Il suffit d'observer que les triangles $(L2,I_n',L1)$ et $(C2,I_n',C1)$ sont proportionnels. Nous avons donc l'équation élémentaire: $$ \frac{D}{d_n'} = \frac{c}{d_n' - d'} $$ où $D$ est la distance $L1L2$. Par définition de l'ouverture nous avons alors: $$D=\frac{f}{a}$$ où $f$ est la distance focale et $a$ l'ouverture. Donc: $$ c = \frac{f}{a} (1 - \frac{d'}{d_n'}) $$ En remplaçant $d'$ et $d_n'$ par leurs valeurs en fonction de $d$ et $d_n$: $$ c = \frac{f^2}{a} \frac{d - d_n}{d_n(d - f)} $$ On peut alors exprimer $d_n$ en fonction des autres paramètres: $$ d_n=\frac{d}{1 + a \frac{c}{f}\frac{d-f}{f}} $$
Le même calcul peut être fait pour un objet OfIf (f signifie far , loin en anglais) qui est plus loin du centre optique que OI. Ce travail est laissé au lecteur comme exercice. Le résultat est: $$ d_f=\frac{d}{1 - a \frac{c}{f}\frac{d-f}{f}} $$
La profondeur de champ d'une lentille de focale $f$ pour une distance de mise au point $d$, avec une ouverture $a$ et un cercle de confusion de diamètre $c$ est la différence $d_f-d_n$: $$ dof = d_f - d_n = 2 d a \frac{c}{f}\frac{d - f}{f} \frac{1}{1 - \left(a\frac{c}{f}\frac{(d-f)}{f}\right)^2} $$
Notons également que le terme définissant $d_f$ devient infini (le numérateur s'annule) à partir d'une certaine combinaison de paramètres $(c,a,d,f)$ bien choisis, rendant également la profondeur de champ infinie. Si l'on considère $(c,a,f)$ comme fixes, la valeur de $d$ qui rend $d_f$ infinie en annulant le dénominateur s'appelle la distance hyperfocale. Nous y reviendrons.
La formule ci-dessus a une approximation très simple quand $d$ est nettement plus grand que $f$ et que nous sommes loin de l'hyperfocale: $$ dof = 2 c a \frac{d^2}{f^2} $$
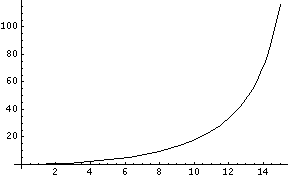
La profondeur de champ varie linéairement en fonction de l'ouverture et de la taille du cercle de confusion, alors qu'elle varie quadratiquement en fonction de la distance au centre optique et à l'inverse de la focale. On peut voir sur les deux courbes suivantes la variation de la profondeur de champ en fonction de l'ouverture et de la distance.
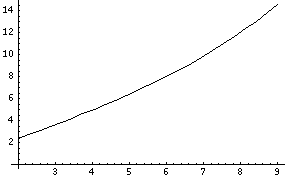
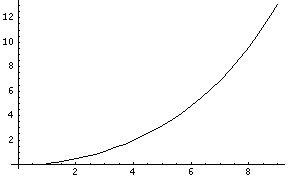
Cela n'est évidemment valide que loin de l'hyperfocale. Dès que l'on s'en rapproche, les courbes prennent une autre forme:
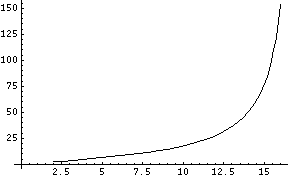
Interprétation photographique et applications numériques
Un exemple pour la photographie numérique
La question fondamentale qui se pose est la suivante: quelle est la taille admissible du cercle de confusion telle que un objet apparaîtra net même s'il n'est pas exactement à la distance de mise au point? La réponse dépend du grain du film ou, dans le cadre de la photographie numérique, de la distance entre les éléments du capteur Nous allons prendre un exemple avec trois appareils différents, un EOS 1Ds Mark II (reflex numérique plein format 36x24mm, résolution de 5000x3200 pixels), un Minolta Dimage A1 ("bridge" avec un capteur de 8.8x6.6mm et une résolution de 3200x2400 pixels) et un EOS 300D (reflex numérique équipé d'un capteur de taille "APS" soit 22x15mm et une résolution de 3000x2000 pixels).
L'objet photographié est situé à une distance d=10m et l'ouverture est réglé sur a=10. nous utilisons une lentille de distance focale f=100mm sur l'EOS1DsMII. Comme nous souhaitons avoir la même photographie avec les trois appareils, la distance focale va être réduite par le facteur de réduction (cropping factor)propre à chaque capteur. Les distances focales à employer seront donc approximativement de 60mm sur l'EOS-300D et 25mm sur le Dimage A1.
Nous prenons comme taille maximale du cercle de confusion la longueur du capteur divisée par le nombre de pixels suivant cette longueur. De cette façon, le diamètre du cercle de confusion reste inférieur à la taille d'un élément, et le flou sera donc indétectable. Pour le 1DsMII nous avons c=(36E-3)/5200=7.2E-6, pour le 300D c=22E-3/3000=7.2E-6 et pour le A1 c=8.8E-3/3246=2.7E-6.
Le calcul de la profondeur de champ donne les résultats suivants:
- EOS 1Ds:
- df = 10.76m
- dn = 9.33m
- dof = 1.43m
- EOS 300D:
- df = 12.48m
- dn = 8.34m
- dof = 4.14m
- Dimage A1:
- df = 17.57m
- dn = 6.99m
- dof = 10.58m
Comparons maintenant quatre appareils plus modernes:
- Le PhaseOne P65+, avec un capteur de 54mm de côté pour 8984 pixels
- Le Canon 5D MarkII, avec un capteur de 36mm de côté pour 5616 pixels
- Le Canon 50D, avec un capteur de 22mm de côté pour 4752 pixels
- Le Canon G10, avec un capteur de 7.6mm de côté pour 4416 pixels
Voici les résultats avec un objectif de 100mm de focale (en 35mm), adapté aux différents formats pour avoir le même cadrage et une ouverture de f/2.8
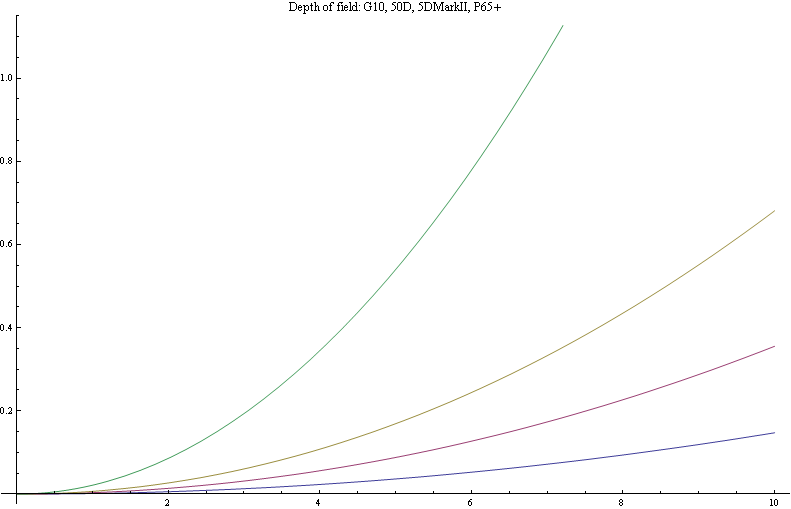
Voici maintenant les résultats si nous ouvrons chaque objectif de façon à avoir l'image la plus piquée possible, c'est à dire f/9 pour le P65, f/10 pour le 5D MarkII, f/7 pour le 50D et f/2.8 pour le G10.
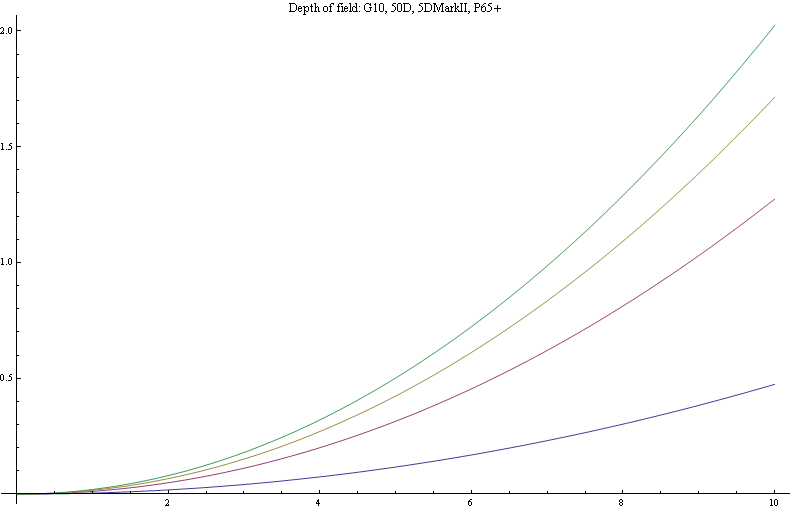
Enfin, rappelons nous que les résultats ci-dessus sont valables si nous regardons les images sur un écran d'ordinateur à 100% de leur taille. Si nous les imprimons sur des papiers de même taille, les résultats sont différents.
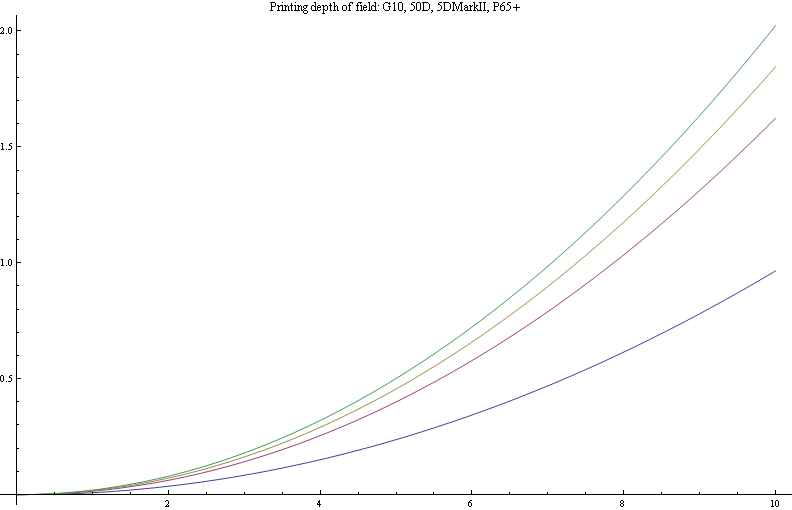
On retiendra que le P65+ reste dans une classe à part. En revanche, les trois autres appareils ne se comportent pas tellement différemment en ce qui concerne la photographie de paysage au niveau de la profondeur de champ (le problème serait très différent pour des portraits, évidemment).
Un exemple pour un ancien appareil manuel, le Minox GT-E
Le Minox GT-E était un appareil à mise au point manuelle et à focale fixe (35mm). Il utilisait un film classique 24x36, à ne pas confondre avec les petits minox qui utilisaient du film 8x11. La profondeur de champ pouvait se lire en combinant les informations de la bague de distance externe (noire) et de la bague rouge intérieure. Sur cet exemple, quand la distance de mise au point était de 3m, tout était net de 2 à 5m avec une ouverture de f5.6, alors qu'avec une ouverture de f16 tout était net de 1.4m à l'infini. On peut calculer le cercle de confusion admissible à partir des données ci-dessus. La formule donnant le cercle de confusion est: $$ c = \frac{f^2}{a} \frac{d_f - d}{d_f(d - f)} $$ Elle peut être approximée (pour $ d \gt f$) par: $$ c = \frac{f^2}{a} \frac{d_f - d}{d_f d} $$
Une application numérique simple ($d=3, d_f = 5, a = 5.6, f = 0.035$) nous donne alors $c=30.10^{-6}$. Cette valeur est absolument consistante avec les valeurs utilisées classiquement en photographie argentique; Les tables de profondeur de champ sont en effet calculées pour le film argentique sur la base d'un cercle de confusion de 33 microns, et ce depuis les années 30. Nous reviendrons sur le choix de cette valeur plus loin.

Sur les appareils à mise au point manuelle, les échelles de profondeur de champ étaient d'une grande utilité, en particulier pour les photographies de paysage avec un premier plan.
L'hyperfocale
La distance hyperfocale (ou hyperfocale) était également une notion importante avec les appareils à mise au point manuelle. Rappelons que la distance hyperfocale est la valeur $d_h$ qui annule le dénominateur de la formule donnant la valeur de $d_f$ Donc: $$ 1 - a \frac{c}{f}\frac{d_h-f}{f}=0 $$ Soit: $$ d_h=\frac{f^2}{ca}\left(1+a\frac{c}{f}\right) $$ Qui peut généralement s'approximer en: $$ d_h=\frac{f^2}{ca}$$
Par exemple, le Minox GT-E à f/16 a une hyperfocale à un peu moins de 3m. On peut la trouver facilement en plaçant le symbole "infini" en face de l'ouverture et en lisant la distance au milieu de la bague. Lorsqu'un appareil est réglé sur l'hyperfocale, tout est net de $d_n$ à l'infini. Cette valeur était particulièrement importante sur les appareils à mise au point manuelle (comme le Minox), ou même sur certains appareils télémétriques (comme les Leica M, Bessa, et autres) lorsque l'objectif utilisé n'était pas couplable au télémètre (par exemple les Voigtlander 12mm, 15mm, etc). Dans ce cas, pour photographier un paysage, il suffisait de régler la distance sur l'hyperfocale, sans avoir besoin de faire une évaluation compliquée de l'éloignement de l'objet.
Comme le montre la formule ci-dessus, l'hyperfocale varie comme le carré de la focale et l'inverse de l'ouverture. Pour photographier un paysage, une hyperfocale est d'autant plus intéressante qu'elle est petite, et il vaut mieux utiliser de grandes ouvertures et des objectifs de courte focale (résultat de bon sens pour tout photographe...) Il n'en va évidemment pas de même pour un portrait...
Quelques éléments de physiologie de l'oeil
L'oeil est composé de plusieurs zones, la plus importante concernant la vision fine des objets est la fovéa, située au centre de l'oeil. La fovéa est une zone relativement petite (environ 3mm de diamètre), qui contient une très forte densité de récepteurs. Sur le diamètre de la fovéa, il y a environ 300 récepteurs, soit environ une densité d'un récepteur tous les 10 microns (les autres zones de l'oeil sont essentiellement dédiés à la vision périphérique: détection des mouvements, et récepteurs essentiellement noir et blanc). La taille d'un "photosite" est donc de 10 microns pour l'oeil.
L'oeil ayant une distance focale de l'ordre de 25mm. Si nous regardons un objet situé à 25 cms de l'oeil (distance standard de lecture), la taille d'un objet couvrant exactement un photosite de l'oeil est: $$ s= O'I' \frac{f}{d} = 0.25 \frac{10.10^{-6}}{25.10^{-3}} = 100\ \mathrm{microns} $$ Le pouvoir de résolution de l'oeil à 25 cms est donc d'environ 100 microns (1/10 de mm).
Supposons maintenant que nous ayons pris une photo sur un négatif 24x36, et que nous l'agrandissions d'un facteur 3 pour obtenir un positif de taille 108x72 (format "standard" d'une photo). Si nous regardons cette photo à une distance de 25 cms, l'oeil ne saura pas distinguer des détails de moins de 100 microns, ce qui correspond à 33 microns sur notre négatif 24x36, taille maximale du cercle de confusion. C'est cette valeur qui a été utilisée pendant des années pour calculer les tables de profondeur de champ pour les films 24x36. Pour des films plus petit (comme le film 8x11 des petits Minox), il fallait agrandir d'un facteur 10, et donc avoir un cercle de confusion de l'ordre de 10 microns. Cependant, les films se contentant d'un pouvoir de résolution de l'ordre de 15 microns, c'est cette dernière valeur qui était utilisée pour les tables de profondeur de champ (pour les films moyen format, on employait une valeur de 60 microns).
Ces valeurs restent correctes pour des agrandissements plus importants, car la distance à laquelle on les regarde est aussi plus importante. Ainsi, pour une projection de diapositive sur un écran de 2mx1.5m, on agrandit l'image environ 60 fois et nos 33microns donnent un cercle de confusion de l'ordre de 2mm. Comme par le plus grand des hasards, la distance de visionnage conseillée est égale à deux fois la diagonale de l'écran soit, 2x2.5m=5m. A 5m, le pouvoir de résolution de l'oeil est 20 fois plus faible qu'à 25 cms (5/0.25=20): il est donc de 100x20=2000 microns = 2mm. Formidable!
On voit clairement que la résolution des appareils numériques est supérieure à ces fameux 33 microns. Le 1Ds MarkII, avec son capteur plein format, à une taille de photosite de 7.2 microns, plus de 4 fois inférieure à la valeur de référence. Pour un A2, la taille du capteur est le quart d'un négatif 24x36, il faut donc passer de 33 à 33/4 ≅ 8 microns, et le A2 dispose de photosites de 2.6 microns. Ceci dit, il faut se rappeler que le capteur est une alternance de photosites Rouge, Vert et Bleu, et que la résolution n'est donc pas égale à la taille d'un photosite...
Il faut également remarquer que les films haut de gamme, comme le défunt Velvia 50 avait une résolution d'environ 40 paires de lignes par mm, soit environ 12.5 microns, une valeur encore une fois très inférieure à 33 microns.
La profondeur de champ vue par l'autre bout de la lorgnette
Jusqu'ici nous nous sommes intéressés à la profondeur de champ pour
savoir ce qui était net. Maintenant, nous allons nous intéresser au
problème dual, qui consiste à rendre volontairement des objets
flous. Cela est particulièrement utile lorsque l'on réalise des
portraits,et que l'on veut faire "disparaître" certains objets de
l'arrière plan.
On a dit pas mal de choses sur la profondeur de champ et les
portraits, qui sont souvent à moitié justes, ou à moitié fausses...
Distance focale et approximation de l'hyperfocale
On a coutume de dire que pour réaliser un portrait, il faut utiliser un objectif de focale plutôt longue, pour diminuer la profondeur de champ. C'est à la fois faux, et vrai...
Lorsque l'on prend une photo, l'agrandissement vaut: $$ \frac{O'I'}{OI} = \frac{f}{d-f} $$ On peut raisonnablement approximer cette formule en $$\frac{O'I}{OI} = \frac{f}{d}$$ tant que $d$ est nettement plus grand que $f$ (ce qui sera vrai, sauf dans le cas très particulier de la macro-photographie, qui de toute façon doit se traiter séparément).
Cetteformule signifie que la taille de l'image sur le film est égal à la taille de l'objet multiplié par $f/d$. Donc, si vous utilisez un objectif de 30mm au lieu d'un objectif de 300mm, il faudra vous placer 10 fois plus près pour garder la même taille à l'image sur votre pellicule. $f/d$ doit donc rester constant pour que l'image garde une taille constante. Or la profondeur de champ loin de la distance hyperfocale est proportionnelle à $d/f$, puisqu'elle vaut environ: $$ dof = 2 c a \frac{d^2}{f^2} $$ En conséquence, la profondeur de champ sera la même quelle que soit l'objectif que vous utilisez, loin de l'hyperfocale .
Voici donc un superbe résultat, qui doit cependant être tempéré. Tout d'abord, avoir la même profondeur de champ avec un objectif de 30mm et un objectif de 300mm ne donnera pas le même résultat en terme de flou des objets qui ne sont pas dans le champ net. Nous discuterons ce point (relativement complexe) dans le paragraphe suivant.
D'autre part, l'arrivée des appareils photos numériques compacts a totalement modifié la donne en matière de profondeurs de champ. Prenons un exemple simple avec quelques valeurs numériques. Supposons que je fasse un portrait en plan américain. L'objet (vilain mot dans ce cas...) que je photographie occupe environ 1m (de la taille au sommet de la tête, avec un peu d'espace au dessus). Pour le faire rentrer exactement sur un capteur 24x36 comme celui d'un EOS 1Ds MarkII avec un objectif de 80mm, je dois me placer à une distance de: $$ d = f \frac{OI}{O'I'} = 80.10^{-3} \frac{1}{36.10^{-3}} = 2.22m $$
La distance hyperfocale pour cet objectif et cet appareil (avec un cercle de confusion de l'ordre de 7.2 microns) est de: $$ d_h = \frac{f^2}{c a}= \frac{(80.10^{-3})^2}{7,2.10^{-6}a}=\frac{842}{a} $$ où $a$ représente l'ouverture. Pour une ouverture de f/16, l'hyperfocale est à 50m.
Si j'utilise maintenant avec le même appareil un objectif de 24mm, je dois me placer à une distance de: $$ d = f \frac{OI}{O'I'} = 24.10^{-3} \frac{1}{36.10^{-3}} = 0.66m $$ La distance hyperfocale devient: $$ d_h = \frac{f^2}{c a}= \frac{(24.10^{-3})^2}{7,2.10^{-6}a}=\frac{80}{a} $$ Toujours avec une ouverture de f/16, la distance hyperfocale est de l'ordre de 5m, et je reste donc bien dans l'approximation classique où l'on reste loin de l'hyperfocale.
Si je fais le même calcul avec un appareil compact utilisé en position grand angle, ma distance focale est de l'ordre de 6mm et je dois toujours me placer à environ 0.66m pour remplir mon capteur. Les photosites sont également plus petits (de l'ordre de 2.7 microns) et la distance hyperfocale pour ce type d'appareil est donc: $$ d_h = \frac{f^2}{c a}= \frac{(6.10^{-3})^2}{2,7.10^{-6}a}=\frac{13}{a} $$ Il faut donc que je fasse attention à ne pas choisir une ouverture trop petite, car on se rapprocherait alors dangereusement de l'hyperfocale, et l'approximation sur la profondeur de champ deviendrait fausse.
Moralité: Les appareils numériques compacts à petit capteur (smartphones) ont des profondeurs de champ énormes, et des hyperfocales très courtes. Si l'on veut réussir un joli portrait avec un arrière plan flou, il vaut mieux ne pas régler l'appareil en position grand angle!
Composer un portrait, et rendre un arrière ou un avant plan flou
Lorsque l'on réalise un portrait, l'on souhaite en général rendre les objets placés en arrière plan flous. Toute la question est de savoir ce qu'est un objet flou.
La définition duale consistant à dire qu'un objet est flou lorsqu'il n'est pas net (et donc hors de la profondeur de champ) n'est pas toujours satisfaisante. En effet, un objet de grande taille, même placé hors de la zone "nette", restera parfaitement reconnaissable, et pourra dénaturer le résultat que l"on souhaitait atteindre. Nous avons donc besoin d'une autre notion de flou, qui dépendra bien sûr de la profondeur de champ, mais aussi de la taille de l'objet que l'on souhaite rendre flou.
Ressources en ligne
L'excellent livre The Ins And Outs Of Focus d'Harold Mecklinger que j'ai découvert relativement tardivement, et dont je ne partage pas la totalité des conclusions, mais qui est une référence.
Le téléchargement ou la reproduction des documents et photographies
présents sur ce site sont autorisés à condition que leur origine soit
explicitement mentionnée et que leur utilisation
se limite à des fins non commerciales, notamment de recherche,
d'éducation et d'enseignement.
Tous droits réservés.
Dernière modification: 11:34, 20/03/2024