Ondes planes

Eléments de base

Nous avons tous une représentation intuitive des ondes. Tout le monde a jeté une pierre au centre d'un bassin. Cela crée une vague: l'eau bouge de façon périodique. De la même façon, le son n'est rien d'autre qu'une vibration de l'air.

Il existe deux grandes catégories d'ondes, les ondes planes et les ondes sphériques (ou circulaires). Une pierre jeté dans un bassin crée une onde circulaire. La même pierre jetée dans un tube étroit va créer une onde plane. Nous allons tout d'abord nous intéresser aux ondes planes.

Lorsqu'une onde se propage, le médium qui sert à porter l'onde ne se déplace par vers l'avant. Seule l'onde "avance". Le médium lui est seulement compressé. Si on met un peu d'huile au centre d'une mare et que l'on jette une pierre au centre de la tâche d'huile, l'huile reste au centre de la mare. Dans une onde, la matière ne se déplace que "verticalement". Seule l'énergie se déplace vers "l'avant".

La façon dont le médium se déplace est décrit mathématiquement par une sinusoïde:

$$ f(r,t) = A\, \cos\left(2 \pi f \left( t - \frac{r}{v} \right) \right) $$

où $t$ représente le temps, $r$ la distance à l'origine, $A$ l'amplitude, $f$ la fréquence, et $v$ la vitesse de propagation de l'onde.

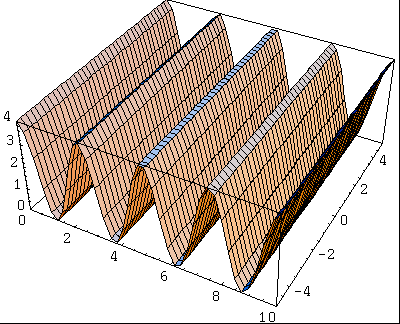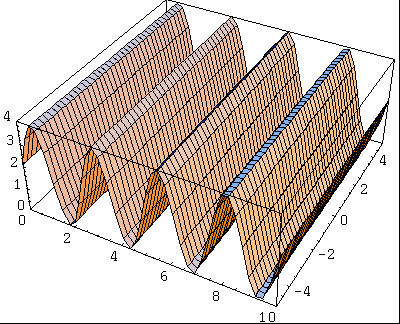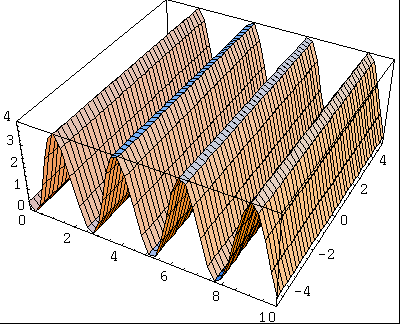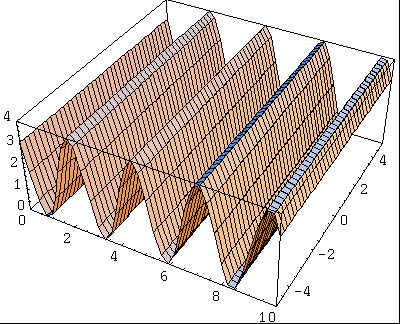
Voici une exemple simple d'onde plane d'amplitude 2.

La distance entre deux maxima (ou minima) est appelée la longueur d'onde (notée généralement $\lambda$), la hauteur des maxima est l'amplitude. Il existe une relation simple entre la fréquence $f$ (le nombre de maxima par secondes), la longueur d'onde $\lambda$ et la vitesse de propagation $v$:

$$ f=\frac{v}{\lambda} $$

La vitesse de propagation d'une onde dépend de plusieurs paramètres (médium transmettant l'onde, température, etc, etc)

L'énergie d'une onde est égale au carré de son amplitude. Pour l'onde précédente, la fonction décrivant l'énergie est donc:

Rappelons encore que le milieu de propagation ne se déplace pas lorsqu'une onde se propage. L'onde se déplace, le milieu de propagation est immobile en moyenne. L'énergie cinétique de la pierre jetée dans la piscine a été largement convertie en énergie mécanique qui permet la création de l'onde.

La façon dont le milieu se déplace est décrit exactement par la fonction sinusoïdale qui décrit à la fois la façon dont le milieu évolue dans le temps à un point $x$ fixé, mais aussi comme l'onde évolué à $t$ fixé en fonction de $x$

Les ondes sonores se comportent exactement comme les autres. C'est l'air qui est mis en mouvement, par exemple par un diapason qui communique sa vibration au milieu. L'onde ainsi créé a une vitesse de transmission de l'ordre de 300m/s (environ 1000km/h, le fameux "mur du son").

Un "la" pur a une fréquence exactement égale à 440Hz, soit 440 vibrations pas seconde. Cette onde est transmise par l'air et atteint notre tympan qui entre à son tour en vibration. Cette vibration est convertie en signal électrique puis transmise au cerveau.

L'oreille peut détecter des signaux qui vont de 20Hz (basse) à 20000Hz (aigu). Cette amplitude dépend de la personne.
Note: si vous vous demandez pourquoi sur certaines chaînes hi-fi on n'emploie qu'un seul haut-parleur pour les basses, comparez simplement les longueurs d'onde; pour un son de 20Hz, elle est de $v/f=300/20=15$ mètres, alors que pour un son de 20000Hz elle est $300/20000=0.015 = 1.5$ cm...

En ce qui concerne les ondes lumineuses, nous verrons que le principe général reste le même: il s'agit également d'ondes, mais électromagnétiques, et l'oeil est le capteur qui transforme la vibration en signal électrique.

Interférence d'ondes planes

Nous allons maintenant nous intéresser à l'interférence de deux ondes planes. Considérons tout d'abord deux ondes identiques, de même amplitude et de même fréquence, et générées au même endroit au même instant. On constate que les ondes se combinent en une onde de même fréquence et d'amplitude double. Son énergie à la forme suivante (en supposant que les ondes avaient chacune une amplitude de 1):

Considérons maintenant deux ondes identiques, mais générés à deux endroits différents, séparés d'une distance égale au quart de la longueur d'onde. L'onde obtenue a la même fréquence que les ondes qui l'ont créé, mais son amplitude dépend de la distance à l'origine. On voit ici la représentation de l'énergie de l'onde résultante:

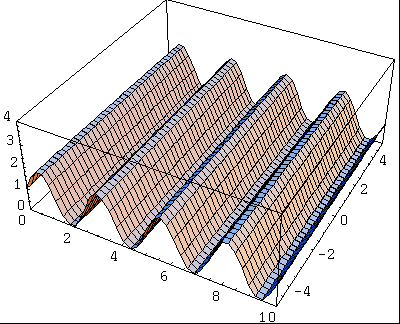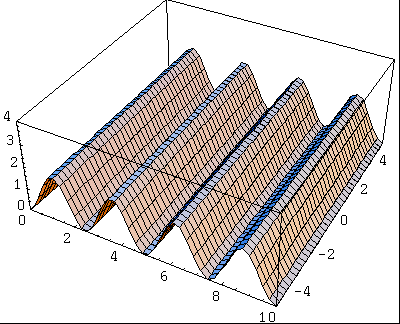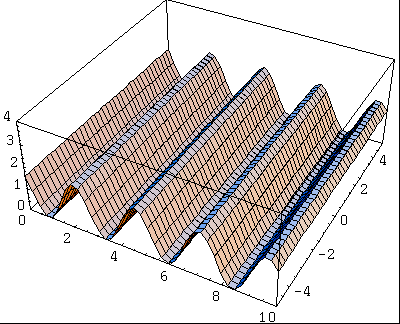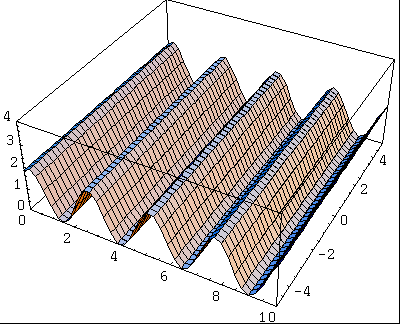
Si l'écart entre l'origine des deux ondes avait été égale à une demi longueur d'onde, l'onde résultat aurait eu une amplitude nulle: il s'agit d'une interférence destructive.

Considérons deux ondes $f(x,t)$ et $g(x,t)$ ayant la même fréquence $f$ et la même amplitude $A$ mais avec deux origines différentes:

\begin{align*} f(x,t)=& A\, \sin \left(2\pi f \left(t-\frac{x}{v} \right) \right) \\ g(x,t)=& A\, \sin \left(2\pi f \left(t-\frac{x-x_0}{v} \right) \right) \end{align*}

Le résultat de l'interférence est donc:

\begin{align*} f(x,t)+g(x,t)=& A\, \sin \left(2\pi f \left(t-\frac{x}{v} \right) \right) + A\, \sin \left(2\pi f \left(t-\frac{x-x_0}{v} \right) \right)\\ =& \,2A\, \cos \left(2\pi f \frac{x_0}{2v} \right) \cos \left(2\pi f \left(t-\frac{x-\frac{x_0}{2}}{v} \right) \right) \end{align*}

L'onde résultante a la même fréquence que les ondes d'origine, mais son amplitude est égale à $2A\, \cos \left(2\pi f \frac{x_0}{2v} \right)=2A\, \cos \left(2\pi \frac{x_0}{2\lambda} \right)$
Donc, pour $x_0=\lambda$, l'amplitude de l'onde résultante est double de celle des ondes d'origine, alors que pour $x_0=\lambda/2$, l'amplitude est nulle: c'est l'interférence destructive parfaite.

Examinons maintenant le cas de l'interférence de deux ondes de fréquence différente. On peut voir ci-dessous l'onde obtenue:

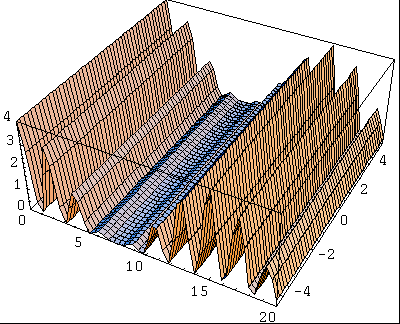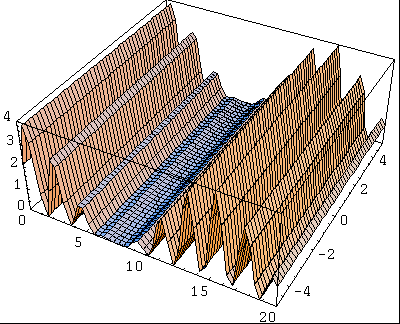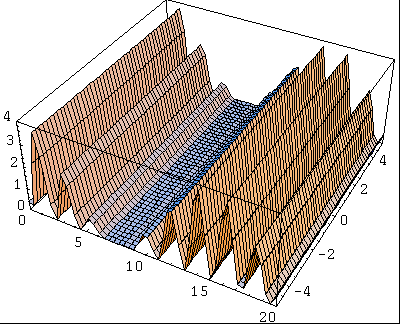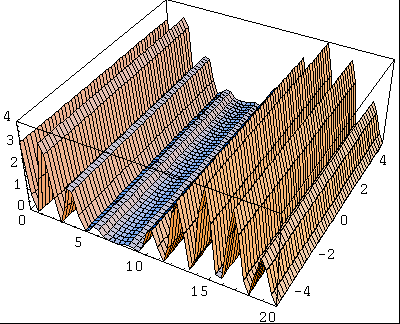
Cette onde dépend bien entendu de la différence entre les fréquences des deux ondes d'origine.

Considérons deux ondes $f(x,t)$ et $g(x,t)$, ayant la même origine et la même amplitude mais deux fréquences $f_1$ et $f_2$ différentes:

\begin{align*} f(x,t)=& A\, \sin \left(2\pi f_1 \left(t-\frac{x}{v} \right) \right) \\ g(x,t)=& A\, \sin \left(2\pi f_2 \left(t-\frac{x}{v} \right) \right) \end{align*}

Le résultat de l'interférence est:

\begin{align*} f(x,t)+g(x,t)=& A\, \sin \left(2\pi f_1 \left(t-\frac{x}{v} \right) \right) + A\, \sin \left(2\pi f_2 \left(t-\frac{x}{v} \right) \right)\\ =& \,2A\, \cos \left(2\pi \frac{f_1-f_2}{2} \left(t-\frac{x}{v} \right) \right) \cos \left(2\pi \frac{f_1+f_2}{2} \left(t-\frac{x}{v} \right) \right)\\ =& \,2A\, \cos \left(2\pi \frac{\delta\! f}{2} \left(t-\frac{x}{v} \right) \right) \cos \left(2\pi f \left(t-\frac{x}{v} \right) \right) \\ \end{align*}

Avec $f=(f_1+f_2)/2$ et $\delta\! f=(f_1-f_2)$
Nous avons une onde dont la fréquence est la moyenne de $f_1$ et $f_2$, mais dont l'amplitude varie avec une fréquence $(f_1-f_2)/2$

Il est important de remarquer que, dans le cas des ondes planes, l'amplitude de l'onde ne varie pas avec la distance à l'origine: si le système est parfait (pas de frottement), il n'y a pas de perte d'énergie et donc pas de modification de l'amplitude. C'est en particulier ce qui permet la transmission d'ondes à l'intérieur de guides d'onde.

Pour les gens qui s'intéressent à l'histoire de l'informatique, les ondes planes générées par des systèmes piezzo-électronique dans des réservoirs remplis de mercure furent un des premiers exemples de mémoire pour ordinateur.

Superposition de plusieurs ondes

Nous ne nous sommes intéressés ici qu'à l'interférence de deux ondes. Bien entendu, un signal, dans le cas général, est composé de plus de deux ondes. Par exemple, une simple corde de guitare lorsqu'elle émet une fréquence fondamentale émet aussi tout un ensemble d'harmoniques. Les harmoniques sont des ondes dont la fréquence est un multiple de la fréquence de base, mais avec une amplitude plus faible. Ce sont les harmoniques qui font la différence entre le "la" émis par un piano, et un "la" émis par une guitare (si les deux ondes étaient strictement identiques, il n'y aurait pas de différence entre les instruments).

La forme d'une onde fondamentale associée à des harmoniques ne ressemble que vaguement à une sinusoïde; sur la figure suivante, nous voyons le mélange de la fondamentale et de six harmoniques, chaque harmonique ayant son amplitude pondérée différemment (la première harmonique est divisée par 2, la seconde par 3, etc):

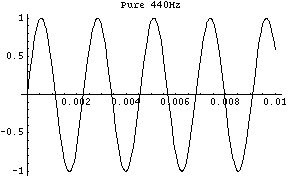
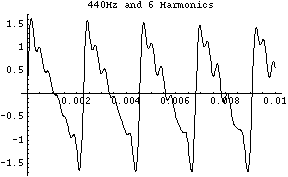
Comme l'oreille humaine n'est sensible qu'aux fréquences inférieures à 20000Hz, les notes aiguës ont moins d'harmoniques audibles, ce qui fait que les notes aiguës sont moins "différentes" d'un instrument à un autre. Le "la" fondamental (440Hz) peut avoir jusqu'à 45 harmoniques, alors que le "la" 5 octaves au dessus (14080Hz) n'aura pas d'harmonique audible (ceci n'est pas tout à fait exact, car un instrument émet aussi des tons inharmoniques qui sont des multiples non entiers de la fondamentale).

Conclusion

Une onde est un phénomène physique qui est essentiellement un transport d'énergie par un médium. La façon dont l'onde se propage est décrit par la fonction d'onde qui, dans les cas simples, est une sinusoïde.
L'interférence entre plusieurs ondes se calcule en faisant la somme des fonctions d'onde.
L'énergie se calcule en prenant le carré de la fonction d'onde.

---

Retour à la page d'accueil.

Le téléchargement ou la reproduction des documents et photographies présents sur ce site sont autorisés à condition que leur origine soit explicitement mentionnée et que leur utilisation se limite à des fins non commerciales, notamment de recherche, d'éducation et d'enseignement.
Tous droits réservés.

Dernière modification: 20:17, 07/03/2024