
Ondes sphériques
Elements de base
Les ondes sphériques, comme, par exemple, celle générée par un caillou tombant au centre d'un bassin, sont différentes des ondes planes. En effet, l'amplitude de l'onde décroît en 1/r lorsque l'on s'éloigne du point origine de l'onde. L'équation générale d'une onde sphérique est:
$$ f(r,t)= \frac{A}{r} \sin\left(2 \pi f (t-r/v)\right) $$Il est assez facile de comprendre pourquoi l'amplitude décroît en fonction de la distance lorsque l'onde se diffuse dans toutes les directions, Il suffit pour cela de considérer le principe de conservation de l'énergie. Le front d'onde augmente au fur et à mesure que l'onde se propage. L'énergie en chaque point du front ne peut donc pas rester constante.
Voici un exemple d'une onde concentrique simple:
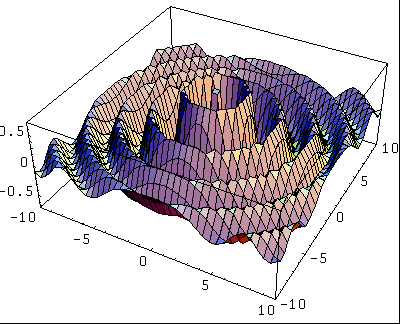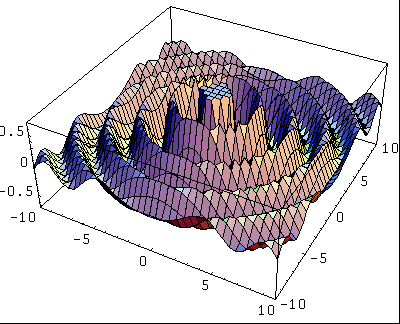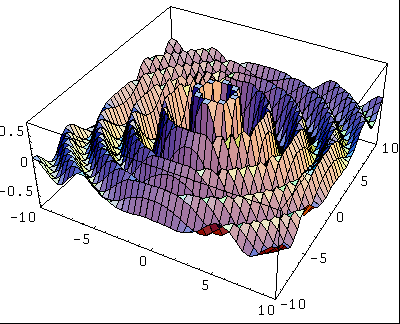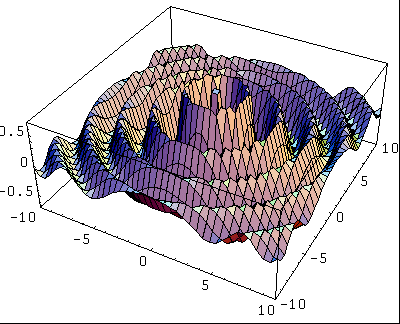
Le point à r=0 est une anomalie. L'onde n'est pas définie en ce point.
Interférences
On calcule l'interférence des ondes sphériques comme on le fait pour les ondes planes. Il s'agit de faire la somme des deux fonctions d'onde. Ci-dessous, on voit l'interférence de deux ondes identiques, avec une distance d'une demi longueur d'onde entre les origines. Le résultat est très différent de ce que l'on observe pour les ondes planes.

L'onde se propage essentiellement le long de l'axe x, alors que l'interférence est essentiellement destructive sur l'axe y.
Résumé
Une onde est essentiellement de l'énergie se déplaçant à travers un milieu, mais pas de la matière en mouvement. Quand deux ondes interagissent, le résultat est parfois contre-intuitif, et s'appelle une interférence. Ce phénomène existe pour toutes les types d'ondes, qu'il s'agisse de vagues, d'ondes lumineuses ou d'ondes sonores.
On peut ainsi faire une expérience très simple: il suffit
d'intervertir les fils d'un des haut-parleurs de votre chaîne hi fi. Le
haut-parleur sera déphasé (il sera en fait en inversion de phase,
c'est à dire que le signal sera décalé d'une demi-période).
Si vous écoutez maintenant un enregistrement monophonique, vous
pourrez constater qu'à certains endroits dans la pièce le son
disparaît, les ondes des
deux haut-parleurs interférant de façon destructive.
Le phénomène d'interférence destructive peut se révéler utile dans
certains cas. Ainsi, en combinant correctement deux antennes, il est
possible de créer des émissions radiophoniques uni-directionnelles. Il
suffit de les séparer d'une demi longueur d'onde.
L'interférence entre plusieurs ondes se calcule en faisant la somme des fonctions d'onde. L'énergie se calcule en prenant le carré de la fonction d'onde.
Le téléchargement ou la reproduction des documents et photographies
présents sur ce site sont autorisés à condition que leur origine soit
explicitement mentionnée et que leur utilisation
se limite à des fins non commerciales, notamment de recherche,
d'éducation et d'enseignement.
Tous droits réservés.
Dernière modification: 20:18, 07/03/2024