Perception de la couleur et colorimétrie

Introduction

La couleur est une des choses les plus physiquement intéressantes, car elle est indissociable de celui qui la regarde. Là où le platonisme tend à pousser les mathématiciens vers la notion d'une réalité objective des mathématiques, et les physiciens vers une réalité objective des lois physiques, la couleur est, elle, indissociable de l'observateur.

Dans toute la suite, les valeurs que peuvent prendre les différentes variables (R, G, B, X, Y, Z, etc) sont comprises de façon continue entre 0 et 1, sauf mention contraire (comme dans le modèle Lab ou le modèle TSL). Nous ne nous occupons pas ici des problèmes de discrétisation liés à la numérisation de l'information

Enfin, pour visualiser correctement cette page, il est fortement conseillé de régler votre moniteur en mode sRGB s'il en possède un. Sinon, vérifiez que votre température de couleur est réglée sur 6500K, que le gamma vaut 2.2 et que le contraste est réglé sur 50% (cette page vous expliquera la signification de ces signes cabalistiques).

Enfin, il serait souhaitable que votre navigateur prenne en compte la gestion des profils colorimétriques. C'est le cas si vous voyez ces deux images comme identiques. Si elles sont différentes, c'est que votre navigateur ne sait pas traiter les profils colorimétriques contenus dans les images (la première image a été sauvegardée avec un profil sRGB, la seconde avec un profil ProPhotoRGB. Affichée de façon "brut de fonderie" sur un moniteur sRGB avec un navigateur n'utilisant pas les profils colorimétriques, la seconde aura une forte dominante violette).

Les versions récentes de Firefox et Internet Explorer prennent automatiquement en charge les profils colorimétriques. Pour les version plus anciennes comme Firefox3, vous pouvez télécharger ici le plugin "Color Management", l'installer puis redémarrer votre navigateur.
Je n'ai pas de solution pour les anciennes versions d'Internet Explorer.

Si votre navigateur ne prend pas en compte les profils colorimétriques, cette page a tout de même de forte chance de s'afficher correctement si vous êtes en mode sRGB.

Couleurs monochromatiques

Il est toujours possible de mesurer expérimentalement une onde lumineuse. Il s'agit en fait d'un mélange (on parle d'un spectre) de plusieurs ondes de longueurs d'onde et d'intensités différentes. Les appareils utilisés pour réaliser ce type d'analyse s'appelle des spectromètres.

Lorsque l'onde lumineuse est réduite à une seule onde avec une seule longueur d'onde, on parle d'onde monochromatique. De telles ondes sont généralement obtenues par l'excitation d'atomes qui, en retombant dans leur état d'énergie fondamental, émettent un photon d'une longueur d'onde précisément déterminée par l'écart entre l'énergie de l'état excité et celle de l'état fondamental (ou de l'état d'énergie inférieur dans lequel ils retombent). Des atomes pouvant avoir plusieurs états excités avec plusieurs énergies différentes, ils émettront des photons de longueurs d'onde différentes, que l'on appelle généralement des raies spectrales. Réciproquement, la connaissance du spectre permet de déterminer le nom de l'atome, une méthode classiquement utilisée en astrophysique.

Voici un extrait du spectre du mercure:

La première raie spectrale (bleue) à une longueur d'onde de 404.6nm, la seconde (bleue) de 435.8nm et la troisième (verte) de 546.1nm. La seconde et la troisième raie ont une importance en théorie de la couleur car elles ont servi de référence pour définir le bleu et le vert dans le modèle colorimétrique RGB de 1931 de la CIE (Commission internationale de l'Eclairage). Le rouge fut défini arbitrairement à 700nm. On remarquera déjà que le vert est en fait légèrement jaune, le rouge "monochromatique" est d'ailleurs légèrement jaune-orangé. En fait, le rouge tel que nous nous le représentons en général n'est pas une couleur monochromatique, il s'agit d'un mélange de rouge monochromatique, et d'une longueur d'onde plus courte dans le bleu-vert.
On voit ci-dessous un extrait du spectre du néon, gaz fréquemment utilisé pour réaliser des éclairages de couleurs, en se concentrant sur les teintes jaunes/rouges:

Toutes les couleurs représentées sont monochromatiques (dans la limite bien sûr de la fidélité de votre moniteur: en fait, si votre moniteur est sRGB, il est en pratique incapable de représenter exactement une couleur monochromatique, nous le verrons plus loin).

Une approche "biologiste" de la colorimétrie

Si nos yeux étaient des spectromètres, ils verraient tout flux lumineux comme un mélange de radiations monochromatiques dont ils analyseraient la fréquence et l'intensité. Mais la vision humaine ne fonctionne pas sur ce mode...

Nous allons utiliser une approche de la colorimétrie qui est très différente de celle utilisée habituellement. La méthode classique consiste à repartir "historiquement" des expériences de Guild et de décrire l'ensemble du processus qui a abouti aux conclusions actuelles sur la vision de la couleur.

Nous allons plutôt de notre coté utiliser une approche "biologique" partant de certains résultats modernes sur la physiologie de l'oeil. La façon dont ces résultats ont été obtenus est de peu d'importance pour notre propos.

Tous les résultats que nous allons utiliser dans les paragraphes suivants portent exclusivement sur la vision photopique, c'est à dire en présence d'un éclairement important, ou vision de jour. Pour la vision de jour, les cellules principalement concernés sont donc les cônes qui se trouvent dans une petite zone au centre de l'oeil dans la fovéa. Ces cellules fonctionnent particulièrement mal la nuit, ce qui donne l'impression que les couleurs disparaissent la nuit, à l'origine de l'expression populaire "la nuit, tous les chats sont gris".

La vision scotopique (ou vision de nuit) fait intervenir d'autres mécanismes et d'autres cellules (les batonnets) dont nous ne parlerons pas ici. On peut voir sur la courbe ci-dessous pour information les deux fonctions de pondération spectrale définies par la CIE (nous verrons plus loin comment) correspondant aux deux types de vision (pour une définition précise de la fonction de pondération spectrale, voir le chapitre sur la photométrie).

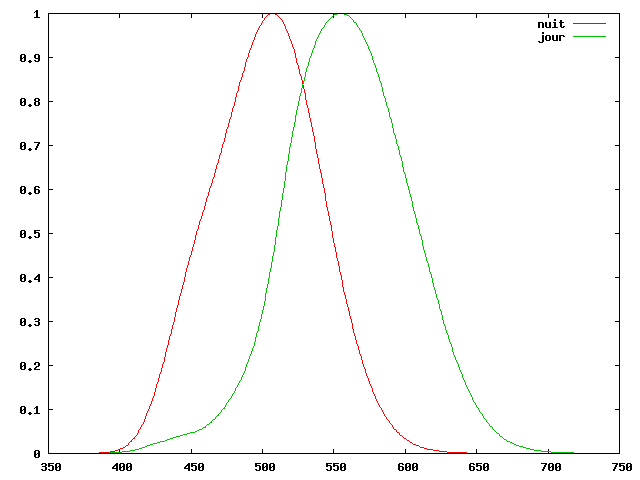
On remarque également une meilleure sensibilité la nuit dans les bleus et une baisse de sensibilité dans les rouges. Une technique très employé dans le monde du cinéma dans les années 80, la nuit américaine consistait à recréer artificiellement la "nuit" en plaçant un filtre bleu sur l'objectif de la caméra.

Nous allons maintenant nous intéresser dans le détail à la vision photopique. Les résultats que nous allons présenter ne sont pas strictement identiques aux résultats expérimentaux de Guild et Wright de 1931, mais les différences sont suffisamment minimes pour être ignorées.

La vision est en fait dépendante de très nombreux paramètres. Tout commence au niveau des récepteurs biochimiques de l'oeil lui-même. En dehors des bâtonnets (qui ne perçoivent pas la couleur), les cellules de l'oeil qui sont responsables de la vision de la couleur sont les cônes. Les connaissances sur la vision ont beaucoup évolué ces dernières années. On sait maintenant qu'il existe trois types de cônes, qui ont des sensibilités différentes, les cônes L, M et S. On peut voir sur le graphique ci-dessous les trois courbes $L(\lambda)$, $M(\lambda)$ et $S(\lambda)$ décrivant la sensibilité énergétique spectrale non normalisée de ces trois types de cônes en fonction de la longueur d'onde.

Ces courbes sont réalisées à partir du travail de Mark Fairchild du RIT Munsell Color Science Lab); elles représentent l'excitation des cônes en fonction de l'énergie reçue de la source (on peut également représenter une sensibilité en fonction du nombre de photons reçues; les deux courbes sont équivalentes dans le principe mais ne se déduisent pas par une simple homothétie: en effet, l'énergie d'un photon est inversement proportionnelle à sa longueur d'onde, et il faut donc multiplier par celle-ci pour passer dune courbe à l'autre).

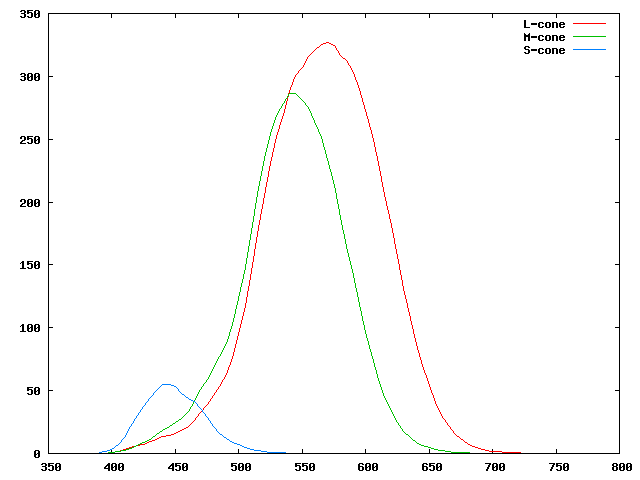
Ces courbes indiquent par exemple que pour une longueur d'onde de 435nm, les cônes seront "excités" suivant le schéma suivant: $(L(435)=11,M(435)=14,S(435)=50)$. Pour une longueur d'onde de 545nm, le schéma devient $(L(545)=300,M(545)=286,S(545)=0)$ et pour une longueur d'onde de 700nm, nous aurons $(L(700)=2,M(700)=0,S(700)=0)$.
Rappelons que nous ne prenons pas ces trois valeurs au hasard; il s'agit des couleurs monochromatiques primaires utilisées par le premier modèle de la CIE, dit modèle CIE-1931.

La sensibilité à la couleur de chacun des types de cônes et des cellules qui les gèrent peut être donc vue comme une sensibilité à un ensemble de radiations centrées autour d'une longueur d'onde. On remarque aussi la faible réponse de l'oeil dans les faibles longueurs d'ondes et le fort recouvrement des courbes de sensibilité des cônes L et M. Ces "spectres de sensibilité" se recouvrent partiellement, et le système d'interprétation des stimuli chimiques travaille par différence, sur un mode de renforcement/inhibition (ce modèle explique en particulier que, si l'on regarde longuement une feuille bleue, puis que l'on regarde une feuille blanche, celle-ci parait légèrement jaune, couleur complémentaire du bleu). Un exemple classique est l'illusion visuelle suivante:

En fixant la croix centrale, on a rapidement l'impression de voir se déplacer un cercle vert (qui est la couleur complémentaire du magenta) alors qu'il ne s'agit que d'une succession d'images dans lesquelles les cercles magentas sont successivement absents (en théorie, on devrait voir tourner un "trou"). La raison pour laquelle il faut fixer la croix centrale est simple: cela oblige les mêmes récepteurs de l'oeil à être sollicités alternativement de façon périodique, alors que si nous fixons le "trou", les recepteurs fixant le trou sont inhibés (ils voient toujours du gris, et l'illusion n'apparait pas). En persistant un peu sur la croix centrale, on peut même au bout d'un certain temps voir disparaitre purement et simplement certains des disques magentas...

Superposition de couleurs monochromatiques

Toutes les sensations de couleurs ressenties par l'oeil en présence d'un faisceau lumineux sont le résultat de l'addition des composantes monochromatiques qui composent ce faisceau. Ainsi, l'addition d'une composante de longueur d'onde 435nm d'intensité 1 et d'une composante de 545nm d'intensité 1/2 donnera une excitation des cônes égales à $(L,M,S)=(11,14,50)+(300,287,0)/2=(161,157,50)$. Ce principe est généralement connu sous le nom de principe de composition linéaire ou parfois loi de Grassmann du nom du mathématicien et linguiste allemand Hermann Grassmann (1809-1827) qui fut le premier à l'énoncer (PS: il existe une autre loi de Grassman, en linguistique, qui a été énoncé par la même personne sur un sujet totalement différent...).

Nous allons maintenant observer ce qui se produit lorsque nous choisissons trois couleurs monochromatiques de base (nous noterons leur longueur d'onde respectivement $(\lambda_r, \lambda_g,\lambda_b)$ et que nous décidons de les superposer avec des intensités arbitraires que nous noterons respectivement $r$, $g$ et $b$. Nous obtenons l'ensemble d'équations suivant fixant les valeurs $l$,$m$ et $s$ de l'excitation des cônes L, M et S: $$ \begin{bmatrix} l\\ m\\ r \end{bmatrix} = \begin{bmatrix} L(\lambda_r) & L(\lambda_g) & L(\lambda_b) \\ M(\lambda_r) & M(\lambda_g) & M(\lambda_b) \\ S(\lambda_r) & S(\lambda_g) & S(\lambda_b) \end{bmatrix} \begin{bmatrix} r\\ g\\ b \end{bmatrix} = P \begin{bmatrix} r\\ g\\ b \end{bmatrix} $$

La matrice $P$ ne dépend que des longueurs d'onde $\lambda_r$,$\lambda_g$,et $\lambda_b$ choisies. La première (resp. seconde et troisième) colonne décrit l'excitation des cônes L, M et S en fonction de la radiation de longueur d'onde $\lambda_r$. Dans le cas général, cette matrice est inversible; si nous notons $Q=P^{-1}$, nous pouvons donc écrire: $$ \begin{bmatrix} r\\ g\\ b \end{bmatrix} = Q \begin{bmatrix} l\\ m\\ s \end{bmatrix} $$

Cette équation nous permet de trouver les intensités $(r,g,b)$ des trois couleurs primaires $\lambda_r$, $\lambda_g$ et $\lambda_b$ en fonction de l'excitation des cônes que l'on souhaite obtenir. Il semblerait donc qu'en utilisant seulement trois couleurs primaires et en modulant leur intensité, on puisse reconstruire n'importe quelle excitation des cônes et donc n'importe quelle sensation de couleur. Cela est évidemment la conséquence directe du fait que l'homme ne possède que trois types de cônes. On dit que la vision humaine est trichromatique. Rappelons encore qu'il s'agit d'un résultat dont la validité est limitée à l'être humain. De nombreux mammifères ont des visions dichromatiques (deux récepteurs) et certains animaux (oiseaux, ou marsupiaux par exemple) sont tétrachromatiques (quatre récepteurs). Pour eux, la représentation des couleurs sur un écran utilisant trois primaires ne correspondrait par à la couleur "réelle" qu'ils perçoivent en regardant l'objet "réel".

Attention: on ne reconstruit pas au sens physique du terme l'onde monochromatique; la seule chose qui est reconstruite c'est la perception visuelle que nous, humains, avons de cette onde monochromatique. Un représentant d'une race venu de Sirius dont l'oeil serait construit avec un plus grand nombre de types de récepteurs ne comprendrait pas plus qu'un spectromètre nos reconstructions à partir de trois primaires. Une fois de plus, les systèmes de représentation de la couleur sont nécessairement adaptés au système de vision de l'observateur.

On voit ci-dessous le principe de mélange des trois primaires additives de ce modèle:

On appelle couleur complémentaire d'une couleur donnée la couleur qui, additionnée à la couleur d'origine, donnera une couleur achromatique (une nuance de gris, qui peut être du blanc). On voit ici que le complémentaire du rouge est le cyan (bleu clair obtenu en mélangeant le vert et le bleu), le complémentaire du vert est le magenta, et le complémentaire du bleu, le jaune.

Ce principe de reconstruction des couleurs par superposition est celui utilisé par les moniteurs vidéo. Si vous disposez d'une loupe de bonne qualité et d'un moniteur LCD, voilà ce que vous verrez en regardant à la loupe une partie blanche de l'écran de votre moniteur:

Cette image (agrandie!) a été obtenu en photographiant un moniteur LCD avec un objectif Sigma macro 105mm EX/DG et un canon EOS 1Ds MarkII. Ainsi, bien que vous ayez l'impression en regardant une page blanche sur votre moniteur que la page est véritablement blanche, vous regardez en fait un ensemble de pixels rouges, verts et bleus.

Fonctions d'équivalence de couleurs ("color matching functions")

Les équations ci-dessus étant toutes linéaires, nous pouvons nous concentrer exclusivement sur la reconstruction des excitations des cônes générées par des couleurs monochromatiques. En effet, en vertu du principe de superposition linéaire (loi de Grassmann) vu plus haut, si nous trouvons les coefficients $(r,g,b)$ permettant de reconstruire toutes les excitations des cônes liées aux couleurs monochromatiques, la recombinaison linéaire de ces coefficients permettra de reconstruire n'importe quelle sensation de couleur.

Nous allons donc construire les fonctions $r(\lambda)$,$g(\lambda)$ et $b(\lambda)$, qui décrivent l'évolution de ces coefficients en fonction de la longueur d'onde. L'équation décrivant ces fonctions est simple: $$ \begin{bmatrix} r(\lambda)\\ g(\lambda)\\ b(\lambda) \end{bmatrix} = Q \begin{bmatrix} L(\lambda)\\ M(\lambda)\\ S(\lambda) \end{bmatrix} $$

Regardons tout cela sur un exemple numérique. Si nous prenons comme valeur des trois primaires 435nm, 545nm et 700nm, la matrice P et son inverse Q sont (rappelons que la matrice P se construit simplement en mesurant l'excitation des cônes L,M et S pour les trois longueurs d'onde choisies): $$ P= \begin{bmatrix} 1.92811 & 300.36447 & 11.14934\\ 0.10506 & 286.66280 & 14.90023\\ 0.00000 & 0.17649 & 50.30185 \end{bmatrix} $$ et $$ Q= \begin{bmatrix} 5.5005\,10^{-1} & -5.7637\,10^{-1} & 4.8812\,10^{-2}\\ -2.0163\,10^{-4} & 3.7003\,10^{-3} & -1.0514\,10^{-3}\\ 7.0743\,10^{-7} & -1.2983\,10^{-5} & 1.9884\,10^{-2} \end{bmatrix} $$

Nous pouvons maintenant représenter les courbes $r(\lambda)$,$g(\lambda)$ et $b(\lambda)$,

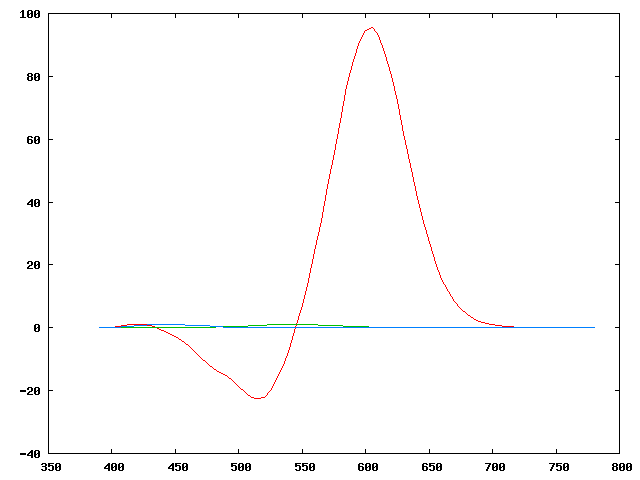
Nous remarquons tout de suite que l'intensité de l'émission dans le "rouge" (700nm) doit être beaucoup plus importante que pour les deux autres composantes. Cela est du à notre choix de primaire: à 700nm, l'oeil est extrêmement peu sensible et la source doit donc émettre une puissance importante. Cela explique d'ailleurs pourquoi ces trois primaires ne sont jamais utilisées dans les systèmes réels (écrans, etc...): leur efficacité spectrale, en particulier dans le rouge, est beaucoup trop faible.
De façon à pouvoir distinguer les courbes plus simplement, nous allons utiliser des échelles différentes et renormaliser ces trois courbes de façon à ce que la surface comprise sous chacune d'entre elle soit la même pour toutes. Nous obtenons alors:

Les trois courbes représentées ci-dessus sont appelées RGB color matching function, et nous les noterons temporairement $r'(\lambda)$, $g'(\lambda)$ et $b'(\lambda)$, Formellement, si nous disposons d'un signal ayant une distribution spectrale $D(\lambda)$, les coordonnées R,G et B dans ce système sont obtenus en calculant les intégrales suivantes: \begin{align*} R &= \int D(\lambda) r'(\lambda) \mathrm{d}\lambda\\ G &= \int D(\lambda) g'(\lambda) \mathrm{d}\lambda\\ B &= \int D(\lambda) b'(\lambda) \mathrm{d}\lambda\\ \end{align*}

Deux signaux $D_1$ et $D_2$ ayant des coordonnées $R$, $G$ et $B$ égales ont la même "couleur" au sens "humain" du terme. En anglais, le nom des fonctions décrit bien leur propriété: si deux signaux ont des coordonnées équivalentes au sens de ces fonctions, alors ils sont "équivalents" (they "match"). Il faut également bien comprendre pourquoi: l'égalité des coordonnées $R$, $G$ et $B$ garantit une excitation équivalente des cônes $L$, $M$ et $S$ de l'oeil, ce qui rend les couleurs indiscernables, même si les distributions spectrales sont différentes. La mise à l'échelle des fonctions $r$, $g$ et $b$ pour passer aux fonctions $r'$, $g'$ et $b'$ ne modifie en rien le résultat, puisque l'on s'est contenté de multiplier de façon uniforme chaque courbe par un coefficient constant.

Espace de couleurs représentables ("Gamut")

Nous voyons qu'il existe une partie du spectre (entre 450 et 550nm) pour laquelle il faudrait générer du rouge négatif pour reconstruire la couleur monochromatique correspondante. Cela est évidemment impossible avec des couleurs primaires réelles, et cette zone est de fait inaccessible de façon exacte avec les trois primaires que nous avons choisies, l'erreur maximale se trouvant aux alentours de 510nm.
On peut représenter dans la zone 400nm->550nm, sur un même graphique, les niveaux d'excitation des cônes $L$, $M$ et $S$ tels que définis par les résultats expérimentaux et les excitations qui seront générées à partir des trois primaires choisies (435nm, 545nm, 700nm), sachant que l'on ne peut générer que des niveaux positifs de ces primaires:

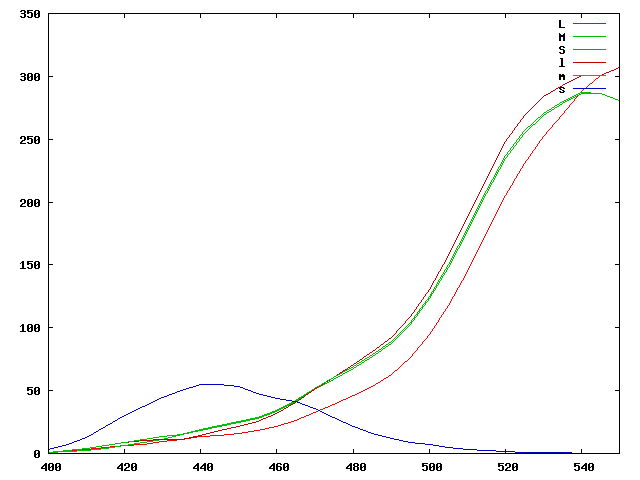
On constate que l'écart principal se trouve sur l'excitation du cône $L$, aux alentours de 510nm comme prévu.

On peut également s'intéresser à la représentation des courbes $r'(\lambda)$, $g'(\lambda)$ et $b'(\lambda)$ sous une autre forme, en posant: \begin{align*} r"(\lambda) &= \frac{r'(\lambda)}{r'(\lambda)+g'(\lambda)+b'(\lambda)}\\ g"(\lambda) &= \frac{g'(\lambda)}{r'(\lambda)+g'(\lambda)+b'(\lambda)}\\ b"(\lambda) &= \frac{b'(\lambda)}{r'(\lambda)+g'(\lambda)+b'(\lambda)} \end{align*}

En se plaçant dans l'espace en trois dimensions $(r",g",b")$ et en traçant la courbe en coordonnées paramétriques, nous obtenons le résultat suivant:

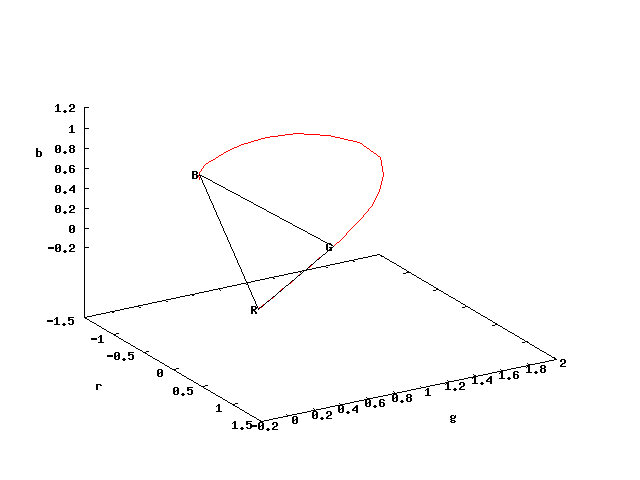
La courbe décrit l'ensemble des valeurs des couleurs monochromatiques; les points $R$, $G$ et $B$ correspondent aux primaires que nous avons choisis (700nm, 545nm et 435nm). On peut projeter cette courbe sur un plan en deux dimensions en n'utilisant que les axes $r$ et $g$, la valeur $b$ étant fixé par la relation $b=1-r-g$.

Les valeurs accessibles par combinaisons linéaires à coefficients positifs des trois primaires $R$,$G$,$B$ que nous avons choisies se trouve dans le quart d'espace ou $r$ et $g$ sont positifs (le triangle noir). On comprend en regardant ces diagrammes pourquoi aucun groupe de trois primaires ne permettrait de couvrir l'ensemble des couleurs visualisables. La courbe est en effet convexe, et il est donc impossible de trouver trois points sur la courbe formant les sommets d'un triangle qui l'engloberait totalement (le fait de changer de primaires revient seulement à changer de base, ce qui peut se ramener à un produit d'homothéties et de rotations, opérations qui maintiennent toutes la propriété de convexité).

Brillance et luminance

La brillance est une mesure objective, comme nous l'avons vu dans le chapitre consacrée à la radiométrie. Nous avons également parlé dans ce chapitre de la luminance, qui est la version photométrique de la brillance. La luminance est obtenue en pondérant un signal lumineux par la fonction de sensibilité spectrale $V(\lambda)$. La courbe de sensibilité spectrale $V(\lambda)$ a été définie expérimentalement par la CIE de la façon suivante:

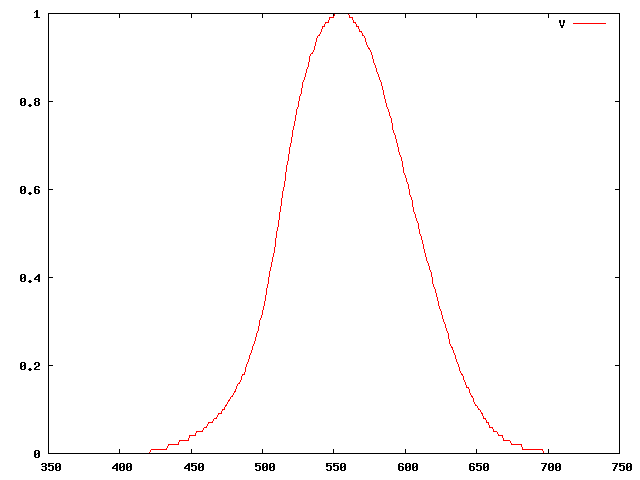
L'oeil n'est donc pas sensible de façon égale à toutes les longueurs d'onde. On pouvait d'ailleurs s'en douter à la vue de la courbe de sensibilité spectrale des cônes de l'oeil. La figure suivante montre les trois couleurs primaires utilisées par votre moniteur.

Le vert semble beaucoup plus lumineux que le rouge, qui est lui-même apparemment plus lumineux que le bleu, alors que les trois couleurs émettent, si on les mesure, la même puissance radiative.

L'importance du vert dans l'information de luminance explique pourquoi les mosaïques Bayer des appareils photos numériques contiennent deux fois plus de capteurs verts que de capteurs rouges ou bleus.

Il faut cependant savoir que l'on sait aujourd'hui que la courbe de luminance "réelle" n'est pas conforme à celle définie par la CIE en 1918. Cette dernière est en effet sous-estimée dans les faibles longueurs d'ondes. Une comparaison amusante consiste à représenter sur un même schéma la courbe V(λ) et la simple somme des sensibilités spectrales des cônes L, M et S:

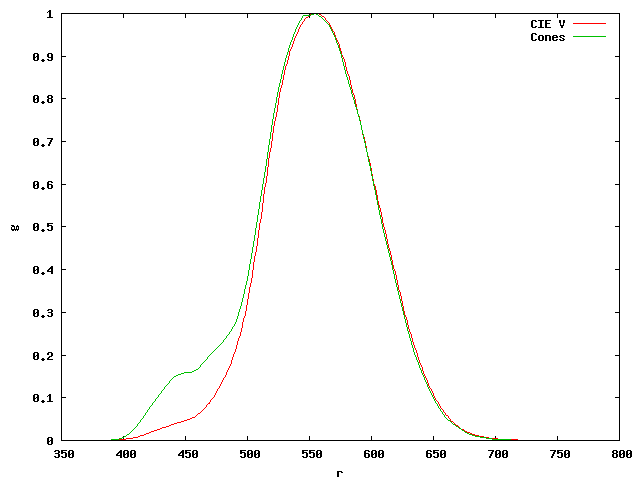
Rappelons également que les composantes dans le modèle RGB d'un signal de distribution spectrale D sont obtenues en calculant les intégrales suivantes \begin{align*} R(D) &= \int D(\lambda) r(\lambda) \mathrm{d}\lambda\\ G(D) &= \int D(\lambda) g(\lambda) \mathrm{d}\lambda\\ B(D) &= \int D(\lambda) b(\lambda) \mathrm{d}\lambda\\ \end{align*}

Rappelons aussi que les fonctions $r$, $g$ et $b$ (nous n'emploierons plus $r''$, $g''$ et $b''$ au niveau de nos notations) sont les fonctions de correspondance de couleur normalisées:

Comment calculer la luminance d'un signal $D$ lorsque l'on ne connaît que ses coordonnées $R$, $G$ et $B$? Nous cherchons en fait l'intégrale: $$V(D) = \int D(\lambda) V(\lambda) d\lambda$$

Il est impossible de calculer strictement cette intégrale si on ne connaît que $R$, $G$ et $B$. En revanche, on peut chercher une solution approchée au problème en cherchant quelle est la combinaison linéaire des courbes $r(\lambda)$, $g(\lambda)$ et $b(\lambda)$ qui approxime le mieux la fonction $V(\lambda)$. Mathématiquement, il s'agit de trouver les valeurs $(a,b,c)$ résolvant le problème de minimisation: $$ \argmin_{(a,b,c)} \int (V(\lambda) - a\, r(\lambda) - b\, g(\lambda) - c\, b(\lambda))^2 $$

Le calcul (trivial avec des moyens modernes) fut effectué par Judd en 1931, avec le résultat normalisé (la somme des coefficients est fixée à 1) suivant: $$V(r,g,b) \cong 0.17697 r + 0.81240 g + 0.01063 b$$

On peut lire ce résultat comme indiquant que dans le modèle RGB CIE-1931, avec les primaires normalisées de ce modèle (435nm, 545nm et 700nm), la composante rouge représente environ 18% de la luminosité, la composante verte 81% et la composante bleue 1%.

Construction formelle du système XYZ

Le modèle XYZ a été défini par la CIE à la suite des travaux de Guild et Wright sur le modèle RGB-1931 dont les primaires étaient 435nm, 545nm et 700nm (le modèle que nous avons déjà décrit ci-dessus). Guild et Wright avaient réalisé une série d'expériences qui avaient abouti au fonctions de correspondance de couleurs de Guild et Wright (Guild-Wright matching functions) qui sont à peu près équivalentes à celles que nous avons construites précédemment à partir des courbes de sensibilité des cônes de l'oeil.

Rappelons encore que les fonctions de correspondance de couleur de Guild et Wright normalisées avaient la forme suivante:

Nous remarquons à nouveau que dans l'espace RGB-1931, un certain nombre de couleurs ne sont représentables qu'en utilisant des composantes négatives pour certaines des primaires, en particulier dans la zone 420-550nm. Rappelons (voir plus haut) que la représentation dans l'espace $(r,g)$ est alors la suivante:

Une des motivations (parmi d'autres comme nous allons le voir) dans la construction du modèle XYZ était de n'utiliser que des composantes positives sur toutes les primaires, quitte à définir des primaires virtuelles.

Nous ne ferons que décrire rapidement les conditions du développement du modèle XYZ. Pour le lecteur souhaitant se documenter plus avant, nous ne pouvons que recommander la lecture de l'excellent article How the CIE-1931 color matching functions were derived from Wright-Guild Data (Fairman, Brill, Hemmendinger, Color Research and Applications, Volume 22, Issue 1, pages 11-23, 1997) ainsi que celle du non moins excellent A Critical Review of the Development of the CIE1931 RGB Color-Matching Functions (Arthur D. Broadbent, Color Research and Applications, Volume 29, Number 4, Aout 2004, pages 267-272) (je ne peux diffuser ces articles car ils sont copyrightés mais on peut se les procurer sur le site de l'éditeur ici et là).

Il est temps maintenant de fixer les conditions formelles du modèle XYZ telles qu'elles furent énoncées au congrès de la CIE de 1931.

1. La loi de Grassmann (superposition linéaire) s'applique
2. Le rapport des coefficients de luminance dans le modèle RGB-1931 est de 1:4.5907:0.0601 (ces rapports se déduisent directement de l'équation de luminance dans le modèle RGB-1931 $$V(r,g,b) \cong 0.17697 r + 0.81240 g + 0.01063 b$$
3. Une des fonctions de correspondance de couleur (la fonction $y$ en fait) est exactement égale à la fonction de luminance $V$
4. Toutes les coordonnées des couleurs "représentables" doivent être positives.
5. Les unités des primaires sont choisis de façon à ce qu'un signal de spectre d'énergie constant aura des coordonnées égales sur les trois axes dans le modèle XYZ.
6. Enfin, le triangle contenant l'ensemble des couleurs représentables doit être le plus petit triangle vérifiant les conditions ci-dessus et tels que ses sommets soient évidemment les primaires virtuelles X, Y et Z.

L'ensemble de ces contraintes conduisait à la construction d'un triangle de ce type:

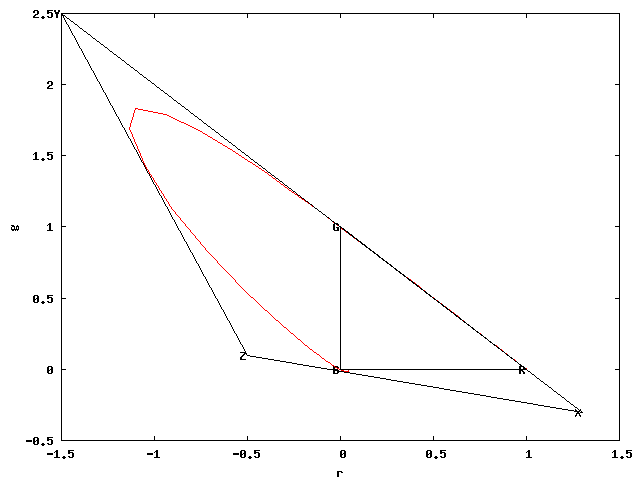
Dans ce schéma, les points $R$,$G$ et $B$ correspondent aux primaires du modèle RGB-1931, les points $X$, $Y$ et $Z$ aux points définissant les primaires virtuelles du système XYZ.

Construire le système XYZ consiste donc à trouver la matrice de passage P' permettant de transformer les coordonnées dans le repère RGB dans les coordonnées dans le repère XYZ: $$ \begin{bmatrix} X\\ Y\\ Z \end{bmatrix} = P' \begin{bmatrix} R\\ G\\ B \end{bmatrix} $$ On peut se contenter de travailler dans le diagramme chromatique en utilisant les coordonnées $x=X/(X+Y+Z)$, $y=Y/(X+Y+Z)$ et $z=1-x-y$, et les coordonnées $r,g,b$ construites de la même façon sur les coordonnées $R,G,B$ (mathématiquement, passer de l'une à l'autre des représentations revient à faire deux projections successives).

Nous n'allons pas détailler par le menu les opérations nécessaires à la construction de la matrice de changement de repère (ou de son inverse). L'article de Fairman suscité décrit par le menu toutes les opérations nécessaires, nous nous contenterons d'indiquer les étapes principales.

• A partir des conditions (2) et (3), on construit l'équation qui doit relier les points X et Z. En effet, la condition (3) impose que les rapports de luminance entre les trois primaires XYZ soient exactement 0:1:0 (toute l'information de luminance est contenue par la fonction y). En conclusion, les points X et Z doivent se trouver sur la droite de luminance nulle, soit $0.17697 r + 0.81240 g + 0.01063 b = 0$. Dans le diagramme chromatique, on a: b=1-r-g, donc l'équation de la droite XZ devient: $0.16634 r + 0.80177 g + 0.01063 = 0.$
• La façon dont fut construite la droite XY est moins claire. Fairman et al. eux-mêmes reconnaissent qu'il ne leur a pas été possible de "trouver une discussion détaillée indiquant comment la pente de cette droite fût choisie". L'explication qu'ils avancent est relativement simple: l'idée initiale avait été de choisir comme droite XY une droite portée par RG . Malheureusement, certaines composantes bleues sont légèrement négatives suivant cette droite, et la condition de positivité avait donc entraîné le choix d'une droite passant par R mais de pente légèrement plus forte, et fixée à 100/99 au lieu de 1.
• Les équations des droites XZ et XY étant connues, il était possible de trouver exactement les coordonnées du points X, qui sont $(1.2749, -0.2777, 0.0028)$.
• Il restait à fixer l'équation de la droite YZ. Il s'agissait d'un problème de géométrie qui fut résolu là aussi de façon rétrospectivement peu transparente. Les coordonnées finales des points Y et Z furent respectivement $(-1.74, 2.7677, -0.0277)$ et $(-0.7430, 0.1408, 1.6022)$. Il faut cependant remarquer que nous n'avons jusque là qu'une transformation qui est valable à un coefficient de proportionnalité près sur chacune des composantes.
• Les conditions (3) et (5) imposent que $$\int x(\lambda) = \int y(\lambda) = \int z(\lambda) = \int V(\lambda)$$ ∫ x(λ) = ∫ y(λ) = ∫ z(λ) = ∫ V(λ), ce qui permet de fixer les coefficients de proportionnalité.

La matrice de transformation fut donc finalement la suivante: $$ \begin{bmatrix} X\\ Y\\ Z \end{bmatrix} = \begin{bmatrix} 0.49000 &0.31000 &0.20000\\ 0.17696 &0.81240 &0.01063\\ 0.00000 &0.01000 &0.99000 \end{bmatrix} \begin{bmatrix} R\\ G\\ B \end{bmatrix} $$

En se plaçant dans le référentiel XYZ, et en utilisant les coordonnées $x=X/(X+Y+Z)$ et $y=Y/(X+Y+Z)$ on obtient la traditionnelle représentation du gamut connue sous le nom du fer à cheval. Dans la figure suivante, le triangle RGB est représenté à l'intérieur du système de coordonnées xyY.

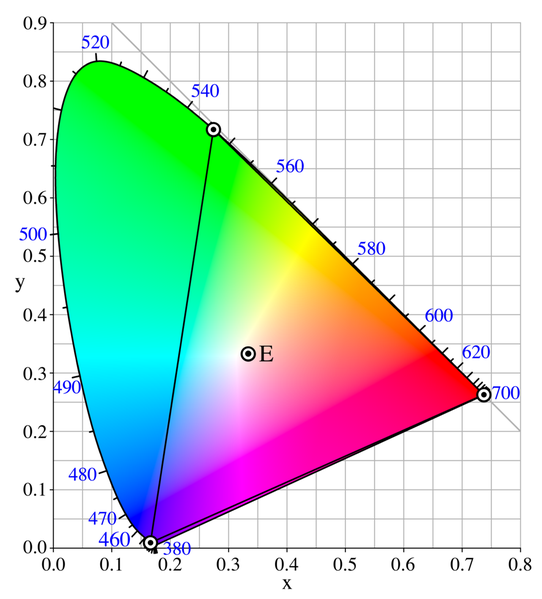
Sur cette figure, l'axe horizontal est désormais l'axe ZX, l'axe vertical est l'axe ZY. Le point $X$ à pour coordonnée $(1,0)$, le point $Y$ $(0,1)$ et le point $Z$ $(0,0)$ dans la projection en deux dimensions que nous utilisons. Le triangle RGB qui définissait le repère orthogonal du système RGB est maintenu "déformé" en raison des rotations et des homothéties introduites par la matrice de passage.

Enfin rappelons que les coordonnées $(r,g,b)$ du modèle RGB-1931 sont obtenues par la multiplication des coordonnées $(l,m,s)$ de l'espace d'excitation des cônes par une matrice de passage P. On a donc: $$ \begin{bmatrix} x\\ y\\ z \end{bmatrix} = P' \begin{bmatrix} r\\ g\\ b \end{bmatrix} = P' P \begin{bmatrix} l\\ m\\ s \end{bmatrix} = R \begin{bmatrix} l\\ m\\ s \end{bmatrix} $$

Le passage de l'espace XYZ dans l'espace LMS est aussi de type linéaire, déterminée par la matrice R, produit des matrices de passage P' et P.

La matrice de passage étant connu, on peut aussi représenter les fonctions de correspondance de couleur dans le modèle XYZ par simple transformation des fonctions de correspondance dans le modèle RGB: $$ \begin{bmatrix} x(\lambda)\\ y(\lambda)\\ z(\lambda) \end{bmatrix} = P' \begin{bmatrix} r(\lambda)\\ g(\lambda)\\ b(\lambda) \end{bmatrix} $$ Ce qui nous donne:

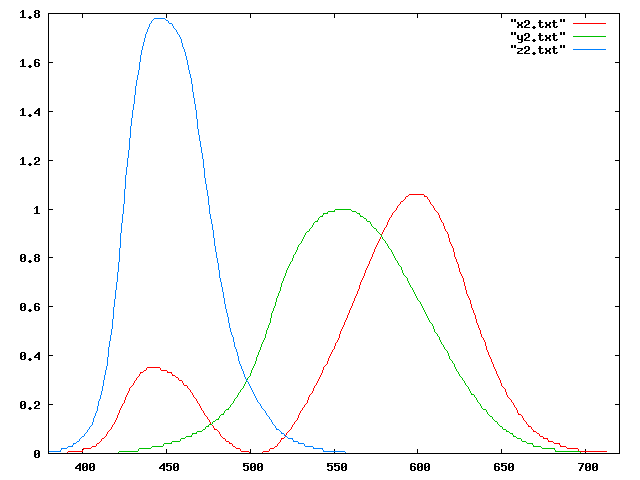
Les fonctions ci-dessus définissent la sensibilité spectrale du modèle. Pour calculer les composantes d'un signal $D(\lambda)$ suivant chacune des primaires XYZ, on mesure au spectromètre son spectre de dispersion de puissance, et on calcule la composante $X$ (resp $Y$ ou $Z$) en pondérant chacune des mesures sur le spectre par le coefficient indiqué sur la courbe $x(\lambda)$ (resp $y$ ou $z$). \begin{align*} X(D) &= \int D(\lambda) x(\lambda) \mathrm{d}\lambda\\ Y(D) &= \int D(\lambda) y(\lambda) \mathrm{d}\lambda\\ Z(D) &= \int D(\lambda) z(\lambda) \mathrm{d}\lambda \end{align*}

PS: Les choses ne sont pas tout à fait aussi simples concernant les trois fonctions de correspondance représentées ci-dessus. En fait, nous avons vu que la fonction y = 0.17696 r + 0.81240 g + 0.01063 b n'est pas en toute rigueur la fonction de luminance V, mais la fonction approchée par la méthode des moindres carrés. La CIE souhaitant absolument que y et V correspondent exactement, les courbes x,y et z subirent une nouvelle (et minime) transformation. Voir Fairman et al. pour plus de détails.

Autres systèmes colorimétriques

Nous allons maintenant regarder de façon formelle et mathématique la définition des différents espaces colorimétriques, qui sont tous définis à partir du modèle XYZ.

Le modèle CIE xyY

Nous avons déjà parlé du système xyY. Il est strictement équivalent au modèle XYZ. Les coordonnées du système xyY sont obtenues à partir du XYZ de la façon suivante: \begin{align*} x &= \frac{X}{X+Y+Z}\\ y &= \frac{Y}{X+Y+Z} \end{align*} La coordonnée $Y$ est conservée. L'intérêt de ce modèle est qu'il calcule des informations de chrominance ($x$ et $y$) qui sont indépendantes de la luminance. L'information de chrominance $z$ est inutile, puisqu'elle peut-être reconstituée par l'équation $x+y+z=1$
La transformation inverse est: \begin{align*} X &= Y \frac{x}{y}\\ Z &= Y \frac{1-x-y}{y} \end{align*}

Les modèles RGB autres que le CIE-1931

Un modèle colorimétrique est toujours défini relativement au modèle CIE xyY ou au modèle XYZ. Il existe deux grandes façons de spécifier un modèle colorimétrique. La première est de le spécifier par la matrice de transformation. Ainsi le modèle RGB CIE Rec709 se définit par la matrice de transformation suivante: $$ \begin{bmatrix} R\\ G\\ B \end{bmatrix} = \begin{bmatrix} 3.240479 &-1.537150 &-0.498535\\ -0.969256 &1.875992 &0.041556\\ 0.055648 &-0.204043 &1.057311 \end{bmatrix} \begin{bmatrix} X\\ Y\\ Z \end{bmatrix} $$

La matrice de transformation contient des coefficients négatifs. Cela signifie que certains points du domaine XYZ sont inaccessibles au modèle RGB-709. Le gamut du modèle RGB-709 est plus petit que celui du modèle XYZ.

Il est intéressant de représenter les courbes de sensibilité spectrale du modèle RGB-709. On les obtient aisément en prenant les courbes de densité spectrale du modèles XYZ et en transformant les coordonnées de chaque point par la matrice ci-dessus. On obtient alors le résultat suivant:

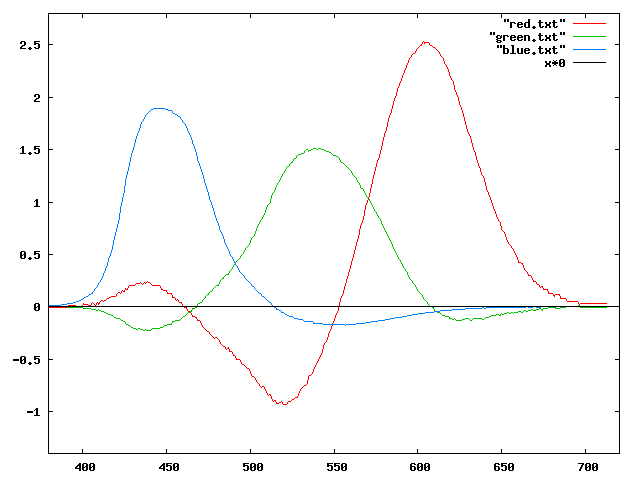
On remarque immédiatement que les courbes obtenues n'ont qu'une lointaine ressemblance avec les courbes de Guild. Cela est parfaitement normal: le système sRGB n'est pas le système RGB-1931 et n'utilise pas les mêmes primaires.

La transformation inverse permet de passer du modèle RGB-709 au modèle XYZ: $$ \begin{bmatrix} X\\ Y\\ Z \end{bmatrix} = \begin{bmatrix} 0.412453 &0.357580 &0.180423\\ 0.212671 &0.715160 &0.072169\\ 0.019334 &0.119193 &0.950227 \end{bmatrix} \begin{bmatrix} R\\ G\\ B \end{bmatrix} $$ Tous les coefficients sont ici positifs: tous les points du domaine RGB-709 sont accessibles dans le modèle XYZ. On voit aussi que, pour le modèle RGB-709, la luminance est définie comme étant constituée par 21% du rouge, 72% du vert et 7% du bleu.

Le gamut du système sRGB a la forme suivante:

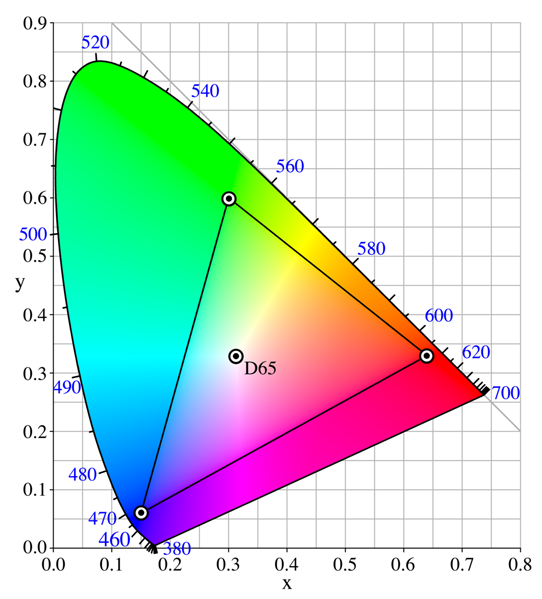
On voit clairement ici que les primaires du système sRGB (les sommets du triangle) ne sont pas des couleurs monochromatiques, mais des couleurs composites ayant des efficacités lumineuses bien meilleures que les primaires RGB du modèle RGB CIE de 1931. Un autre résultat intéressant est que toutes les couleurs monochromatiques sont inaccessibles dans l'espace sRGB (elles sont toutes hors du triangle de Gamut). En fait, sRGB est surtout ce que l'on appelle un "espace moniteur", c'est à dire un espace qui a été conçu pour être utilisé et "efficace" sur des moniteurs vidéo.

Une autre façon de définir un modèle consiste à donner les composantes des primaires dans le modèle Yxy, ainsi que la valeur du "point blanc", c'est à dire du point de coordonnée $[1,1,1]$ (il s'agit ici du point D65; nous reviendrons plus loin en détail sur la notion exacte de point blanc). On retrouve aisément ces valeurs sur le diagramme ci-dessus, les valeurs $(x_r,y_r)$, $(x_g,y_g)$ et $(x_b,y_b)$ correspondant au coordonnées des trois primaires dans le système Yxy. $$ \begin{matrix} &x_r &y_r &x_g &y_g &x_b &y_b &x_w &y_w\\ \mathrm{RGB-709} &0.64 &0.33 &0.30 &0.60 &0.15 &0.06 &0.3127 &0.3290 \end{matrix} $$ Les deux formulations sont équivalentes, et il est très simple de passer mathématiquement de l'une à l'autre en utilisant les formules suscitées. Par exemple, pour retrouver les coordonnées de la primaire rouge, on calcule l'image du point $[1;0;0]$ par la matrice de transformation.
Pour le point blanc, on cherche l'image du point $[1;1;1]$: $$ \begin{matrix} X_w &=&0.412453+0.357580+0.180423& =& 0.9504583\\ Y_w &=& 0.212671+0.715160+0.072169& =& 1.0\\ Z_w &=& 0.019334+0.119193+0.950227& =& 1.088754\\ x_w &=& 0.9504583 / (0.9504583+1.0+1.088754)& =& 0.3127\\ y_w &=& 1.0 / (0.9504583+1.0+1.088754) &=& 0.3290 \end{matrix} $$ La norme Rec-709 est celle utilisée pour définir le modèle sRGB ainsi que le modèle HDTV.

Il existe d'autres modèles colorimétriques RGB. Le tableau suivant définit les caractéristiques des principaux (le point blanc n'est pas précisé, ces modèles admettant tous D65 comme point blanc): $$ \begin{matrix} &x_r &y_r &x_g &y_g &x_b &y_b\\ \mathrm{RGB-709} &0.640 &0.330 &0.300 &0.600 &0.150 &0.060\\ \mathrm{PAL-EBU} &0.640 &0.330 &0.290 &0.600 &0.150 &0.060\\ \mathrm{Apple} &0.625 &0.340 &0.280 &0.595 &0.155 &0.070\\ \mathrm{Adobe98} &0.640 &0.340 &0.210 &0.710 &0.150 &0.060 \end{matrix} $$

Le modèle Adobe-RGB-98 a un gamut plus large que le modèle sRGB. Il est assez régulièrement utilisé sur certains appareils photographiques haut de gamme. Il s'agit d'une forme de "compromis" entre un espace "moniteur" comme sRGB, un espace d'impression comme CMYK (qui est inclus dans AdobeRGB) ou d'un espace de "stockage" tel ProPhotoRGB que nous allons voir ci-dessous (et qui est plus large de AdobeRGB).

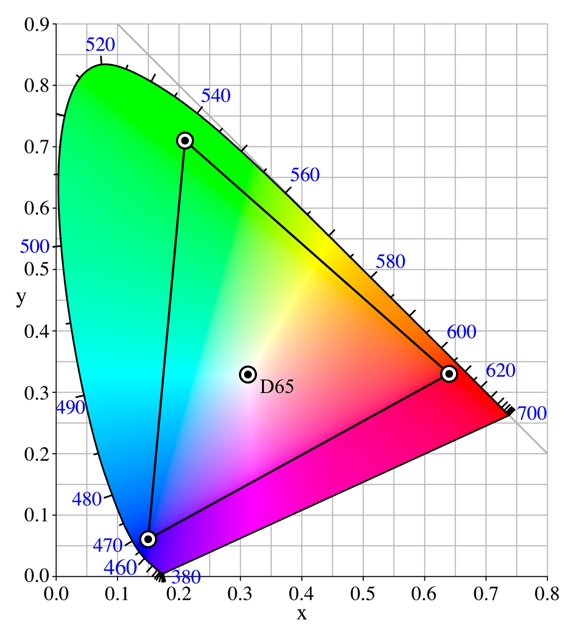
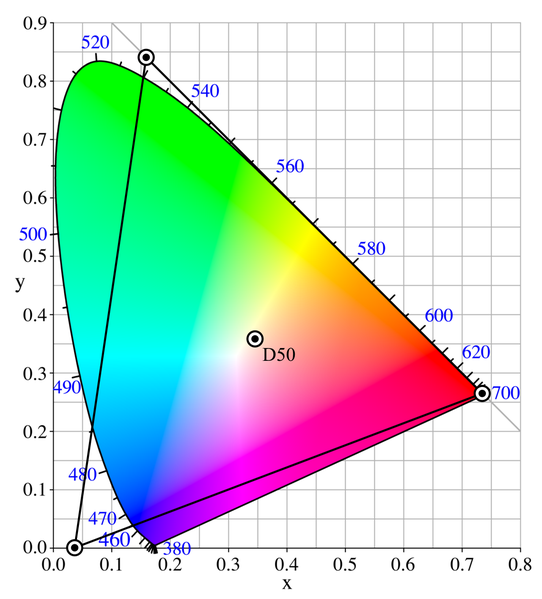
Le modèle ProPhotoRGB, développé par Kodak, a en revanche un point blanc différent, le point D50: $$ \begin{matrix} &x_r &y_r &x_g &y_g &x_b &y_b\\ \mathrm{ProPhoto} &0.735 &0.265 &0.160 &0.840 &0.037 &0.000 &0.346 &0.359 \end{matrix} $$

Le modèle ProPhotoRGB a un gamut encore plus large que le modèle AdobeRGB. Il couvre 90% de la surface des couleurs représentable. En revanche, 13% des couleurs représentables dans ce modèle sont imaginaires (dont 2 des 3 primaires), ce qui implique une perte de précision et un risque de "posterisation" lors du passage de l'espace ProPhotoRGB dans un espace imprimable (vous trouverez ici le profil ICM pour ProPhotoRGB). Il s'agit de l'espace permettant de conserver le maximum de nuances dans un espace de couleurs, mais il est indispensable de travailler avec un codage de couleurs sur 16 bits pour éviter la posterisation. ProPhotoRGB est le modèle idéal (lorsqu'il est utilisé en 16 bits) pour la conservation des photographies, en raison de sa capacité à maintenir un maximum de nuances. Son principal inconvénient est la taille des fichiers 16 bits générés.

Voici par exemple une comparaison des espaces sRGB, AdobeRGB et ProPhotoRGB avec le gamut de l'Epson 3800 sur papier PremiumLuster (images extraites du site d'Eric Chan):

On remarque que seul l'espace ProPhotoRGB contient la totalité du gamut de l'Epson 3800, et que seul cet espace de stockage permettra d'exploiter la totalité des couleurs de cette imprimante.

Le modèle CIE LAB

Ce modèle est plus complexe, car il est non-linéaire, mais il reste inversible. Il est défini par les formules suivantes: \begin{align*} L^* &= \begin{cases} 116 \sqrt[3]{\frac{Y}{Y_n}}-16\ \text{si}\ \frac{Y}{Y_n}\gt0.008856\\ 903.3 \frac{Y}{Y_n}\ \text{sinon} \end{cases}\\ a^* &= 500 \left( f\left(\frac{X}{X_n}\right) - f\left(\frac{Y}{Y_n}\right)\right)\\ b^* &= 200 \left( f\left(\frac{Y}{Y_n}\right) - f\left(\frac{Z}{Z_n}\right)\right)\\ f(t) &= \begin{cases} \sqrt[3]{t}\ \text{si}\ t\gt 0.008856\\ 7.787t+\frac{16}{116}\ \text{sinon} \end{cases} \end{align*} $X_n$,$Y_n$,$Z_n$ sont les valeurs maximales possibles; dans le cas de systèmes d'affichage digitaux, on utilise en général les coordonnées du point blanc du système.

L'axe $a$ va du vert (-128) au rouge (127), et l'axe $b$ va du bleu (-128) au jaune (+127). $L^*$ varie de 0 à 100 et représente la luminosité au sens perceptif, et non plus la luminance. Nous allons revenir sur ce point dans le paragraphe suivant.

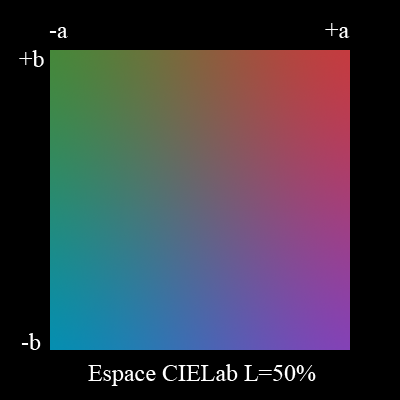
Le modèle CIELab est un modèle relatif. C'est la base du moteur colorimétrique de beaucoup de logiciels graphiques, dont Photoshop.

Le modèle TSL

Le modèle Teinte/Saturation/Luminosité est parfois aussi appelé modèle TSV (V: Valeur). En anglais, cela donne HSV: Hue, Saturation, Value, ou HSL. Il a été créé en 1978 par Alvy Ray Smith. Il est basé sur des notions intuitives: la teinte, la saturation de la teinte (qui correspond à la quantité de blanc que l'on a rajouté; moins il y a de blanc et plus la teinte est pure), et enfin la luminosité. La teinte varie de 0 à 360 degrés, ce qui explique l'expression de "roue colorimétrique" que l'on emploie fréquemment lorsque l'on travaille sur l'espace TSL. La saturation et la valeur (luminosité) varient de 0 à 1. Les coordonnées de l'espace TSL sont donc cylindriques, et on le représente en général ainsi:

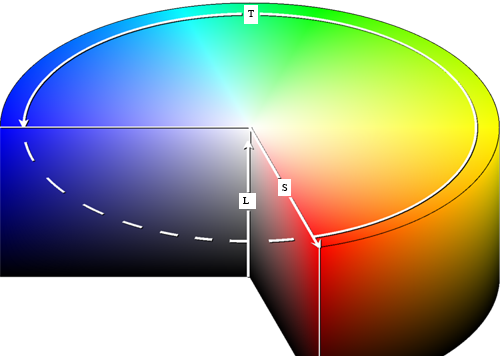
Le modèle TSL est fortement déconseillé par certains auteurs, qui le considèrent imprécis et obsolète. Cependant, son caractère intuitif lui a permis de persister, et il est toujours disponible, non pas comme modèle de base, mais comme moyen de choisir les couleurs, et d'estimer leurs relations respectives. Ainsi, l'outil de choix de couleur de Gimp est particulièrement agréable d'emploi. Le choix de la teinte se fait en tournant le cercle noir dans la roue colorimétrique, ce qui fait tourner le triangle et change les couleurs qu'il affiche. Le choix de la saturation et de la luminosité se fait alors en déplaçant le point blanc à l'intérieur du triangle:

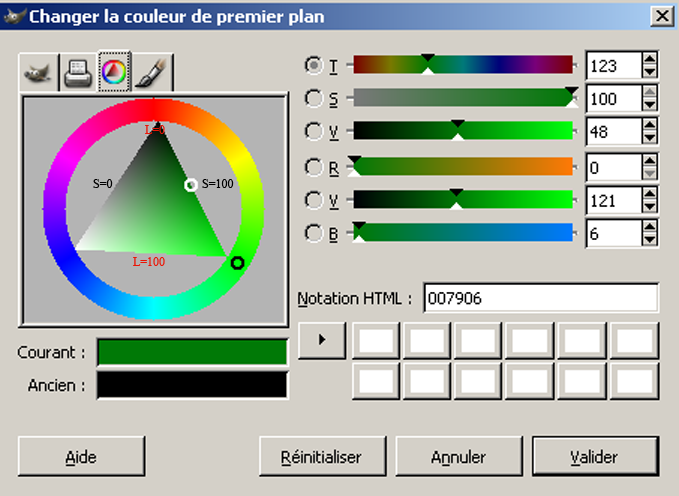
La construction de la couleur complémentaire en mode HSV se fait en tournant la roue colorimétrique de 180 degrés, et en choisissant comme valeur $S'$ et $L'$: $$ \begin{align*} L' &= L (S-1) + 1\\ S' &= S \frac{L}{L'} \end{align*} $$ Attention: les coordonnées en mode HSV ne sont pas additives!

Il n'existe pas de fonction de correspondance matricielle entre le modèle TSL et le modèle XYZ ou un modèle RGB, mais il est facile de définir analytiquement le passage d'un mode à l'autre. Ainsi le passage du mode RGB en mode TSL se fait de la façon suivante: $$ \begin{align*} M &= \max(R,G,B)\\ m &= \min(R,G,B)\\ T &= \begin{cases} \text{non défini si}\ M=m\ \text{(couleur achromatique)}\\ 60 \frac{G-B}{M-m} + 0\ \text{si}\ M=R\ \text{et}\ G\gt B\\ 60 \frac{G-B}{M-m} + 360\ \text{si}\ M=R\ \text{et}\ G\lt B\\ 60 \frac{B-R}{M-m} + 120\ \text{si}\ M=G\\ 60 \frac{R-G}{M-m} + 240\ \text{si}\ M=B \end{cases}\\ S &= \begin{cases} 0\ \text{si}\ M=0\\ 1 - \frac{m}{M}\ \text{sinon} \end{cases}\\ L &= M \end{align*} $$ Le passage du TSL au RVB n'est pas plus compliqué: $$ \begin{align*} h &= \lfloor T/60\rfloor \mod 6\\ f &= T/60 - \lfloor T/60\rfloor\\ p &= L (1 - S)\\ q &= L (1 - f\,S)\\ r &= L \left(1 - (1-f) S\right)\\ \end{align*} $$ $$ \text{Si}\ h= \begin{cases} 0\ \text{alors}\ R=L, G=r, B=p\\ 1\ \text{alors}\ R=q, G=L, B=p\\ 2\ \text{alors}\ R=p, G=L, B=r\\ 3\ \text{alors}\ R=p, G=q, B=L\\ 4\ \text{alors}\ R=r, G=p, B=L\\ 5\ \text{alors}\ R=L, G=p, B=q \end{cases} $$

Le modèle CMJN

Le modèle CMJN (Cyan, Magenta, Jaune, Noir, ou CMYK en anglais) est un modèle soustractif, et non additif.

Il est utilisé en imprimerie, et il décrit le procédé le plus fréquemment utilisé, la quadrichromie. Trois couleurs fondamentales suffiraient à le définir (le Cyan, le Magenta et le Jaune, qui sont les complémentaires des couleurs RGB). Le noir a été rajouté à l'origine pour des raisons de coût (il revenait moins cher de rajouter du noir que de rajouter des proportions égales des trois primaires pour obtenir les nuances de gris). Il y avait également des raisons techniques de miscibilité des encres.

Le modèle CMJN est soustractif car il décrit l'addition de pigments qui absorbent les radiations lumineuses. Le spectre réfléchi étant le complémentaire du spectre absorbé, l'addition d'encres rend le résultat plus sombre. Il s'agit d'un phénomène identique à celui que l'on observe en mélangeant des tubes de couleurs en peinture.

Il faut savoir qu'il existe à peu près autant de modèles CMJN que de systèmes de reproduction de la couleur. Ces systèmes doivent être calibrés pour assurer la meilleure correspondance possible entre les couleurs sRGB et les couleurs CMJN.

En effet, le modèle CMJN a un gamut différent de celui du modèle sRGB. Il est capable de représenter certaines couleurs absentes dans le modèle sRGB , mais il lui manque des nuances d'orange et de rouges, et les bleus "tirent" vers le violet.

Le problème de la conversion d'un espace colorimétrique de travail dans un espace colorimétrique plus étroit pour l'impression sera traité dans le paragraphe suivant.

Il existe des solutions pour les tirages haut de gamme qui permettent de régler une partie des problèmes de la quadrichromie: c'est l'hexachromie, qui ajoute deux couleurs fondamentales supplémentaires: l'orange et le vert (ou le bleu). C'est la société Pantone, qui réalise depuis 1963 un nuancier du même nom, qui est à l'origine du procédé hexachromique dans les années 90. Les imprimantes photo haut de gamme utilisent fréquemment huit (ou plus) encres différentes. On trouvera à la fin de ce document les profils ICC d'imprimante Epson.

C'est parce que les imprimantes modernes ont un gamut plus grand que le gamut sRGB que c'est une mauvais idée de stocker ses photos dans l'espace sRGB. En effet, ces photos ne pourront pas exploiter la richesse du gamut de l'imprimante.

Nous allons maintenant nous intéresser au moyen de passer d'un espace de couleur à un autre quand les gamuts de couleurs ne se recouvrent pas.

Rendu des couleurs entre espace colorimétrique ayant des gamuts différents

L'inconvénient du modèle sRGB est son gamut relativement faible. Le modèle Adobe-RGB permet d'avoir accès à plus de couleurs, en particuliers dans les teintes vert/jaune. On voit ci dessous une représentation des gamuts comparés des modèle sRGB, Adobe-RGB et ProPhotoRGB.

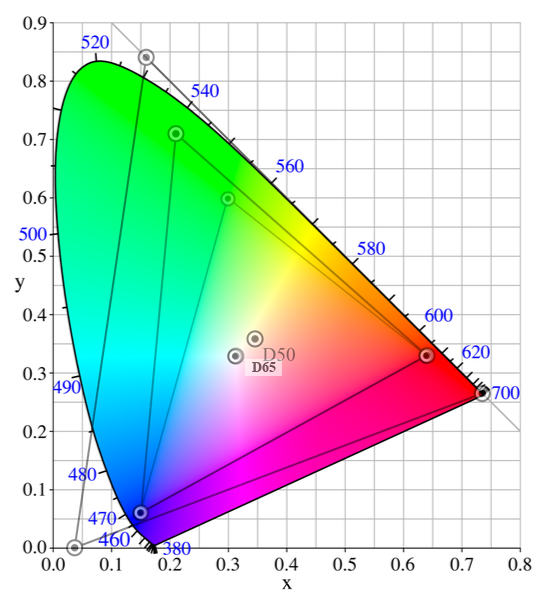
Il faut cependant être extrêmement prudent! Le moniteur sur lequel vous visualisez ce texte est certainement sRGB et il est donc bien incapable de représenter les couleurs du modèle Adobe-RGB. L'illustration ci-dessus n'est qu'une approximation qui permet de se faire une idée des avantages du modèle Adobe-RGB mais il ne s'agit en aucun cas d'une représentation fidèle! Le problème est donc particulièrement difficile à gérer lorsque l'on souhaite éditer une image Adobe-RGB sur un moniteur sRGB...

Il existe une excellente page (en anglais) qui décrit les problèmes de représentation du simple spectre monochromatique sur un écran sRGB. Voici deux représentations possibles extraites de cette page, qui ne sont pas plus fausses l'une que l'autre:

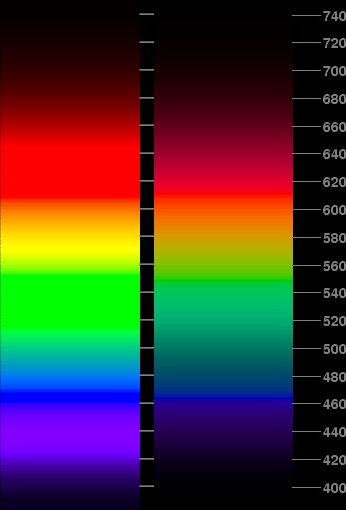
La différence entre les deux résultats vient des choix que l'on fait lorsque l'on décide de représenter l'image.
Le même problème se pose de façon encore plus aigu lorsqu'il s'agit d'imprimer une photographie. Comme dit précédemment, l'espace colorimétrique CMJN d'imprimerie est un espace soustractif, et son gamut est très différent de l'espace sRGB.

Il y a quatre méthodes principales de rendu:

• Le rendu perceptuel essaie de préserver la relation visuelle entre les couleurs de façon à maintenir un résultat aussi naturel que possible pour l'observateur, mais au détriment de la fidélité des couleurs. C'est la méthode utilisé de façon standard dans l'imprimerie japonaise. Elle est plutôt efficace pour les photographies contenant beaucoup de couleurs hors du gamut de l'espace de destination.
• Le rendu saturé produit des couleurs aussi saturées que possible, au détriment de la précision. Cette méthode est surtout utilisée pour les diagrammes et schémas.
• Le rendu colorimétrique relatif compare les couleurs les plus lumineuses des espaces de départ et d'arrivée et déplace les couleurs en conséquence. Les couleurs hors du gamut de l'espace d'arrivée sont transformées dans la couleur la plus proche de l'espace de destination. Cette méthode préserve davantage les couleurs que le rendu perceptuel. C'est la méthode standard en Europe et en Amérique du Nord.
• Le rendu colorimétrique absolu est le plus simple. Il fait une simple transformation mathématique et ramène les valeurs hors du gamut dans l'espace d'arrivée par simple troncature. La fidélité des couleurs qui sont dans le gamut est parfaite, mais les relations impliquant des couleurs hors gamut sont faussées.

On voit ci-dessous la comparaison du gamut sRGB et du gamut CMJN, dans l'espace sRGB bien entendu (les couleurs CMJN non affichables dans l'espace sRGB sont évidemment absentes).

Le spectre CMJN a été réalisé avec un rendu en colorimétrie absolue, puis un rendu perceptuel et un rendu en colorimétrie relative. On voit bien que certaines couleurs comme le bleu du mode RGB n'existent pas en mode CMJN. Dans le cas d'une impression de l'image sRGB, en Europe, le rendu ressemblerait certainement au rendu colorimétrique relatif. Au Japon, ce serait le rendu perceptuel.

Nous discuterons plus bas du fonctionnement détaillé des profils ICC.

Réflectance, point blanc et spectre émissif d'un illuminant

Nous avons jusqu'ici considéré seulement des systèmes émissifs, mais, dans la vie de tous les jours, la lumière émise par un système est la plupart du temps une lumière réfléchie. La majorité des objets qui sont photographiés se contentent de réfléchir la lumière d'une source lumineuse (soleil, flash,...)

On définit pour ce type d'objet un coefficient de réflectance $R(\lambda)$ qui indique la fraction de rayonnement réfléchi pour chaque longueur d'onde du spectre. Un objet ayant un coefficient de réflectance égal à 1 sur tout le spectre sera un objet "blanc", un objet ayant un coefficient de réflectance élevé dans les faibles longueurs d'onde et nul ailleurs apparaîtra bleu, etc...

La question est donc maintenant de définir quel est le type de la source qui va éclairer les objets. Pour qu'un objet blanc apparaisse blanc, il faut que l'illuminant ait exactement comme coordonnées chromatiques les coordonnées chromatiques du point blanc dans le système colorimétrique considéré.

Voyons cela sur un exemple: dans le système sRGB, nous connaissons les coordonnées chromatiques du point blanc qui sont $x_w=0.3127$ et $y_w=0.3290$ par définition. Ce point blanc répond à l'appellation D65. En toute rigueur, un illuminant comme D65 est entièrement déterminé par son spectre de dispersion de puissance. On peut voir ci-dessous le spectre de dispersion de l'illuminant D65 tel que normalisé par la CIE (courbe verte):

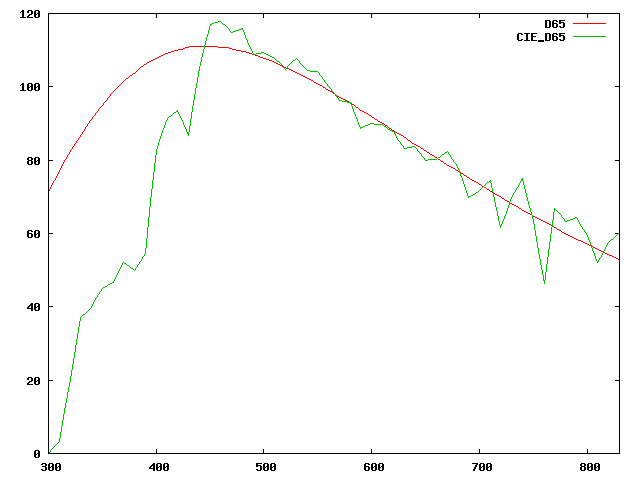
On peut aisément vérifier que le point blanc défini par le spectre de D65 est bien celui qui vérifie R=G=B=1 dans le modèle RGB-709. Pour cela, on prend la distribution spectrale de puissance de D65, puis on la pondère suivant les courbes $r(\lambda)$, $g(\lambda)$ et $b(\lambda)$ du modèle sRGB et on somme le résultat pondéré; on constate alors que les trois valeurs R,G et B obtenues sont égales à moins de 1% près. De la même façon, si on mesurait les composantes chromatiques de D65 dans XYZ, on retrouverait bien les valeurs définies pour le point blanc du système sRGB.

L'illuminant D65 correspond suivant la définition de la CIE à la "lumière provenant d'un ciel bleu exposé au Nord, avec environ 3/5 de nuages blancs épars, vers 10 heures du matin en septembre sous nos latitudes et sans réflexion parasite."

Température de couleur

La définition ci-dessus est cependant très lourde à mettre en oeuvre, et l'on utilise une définition plus simple permettant de définir le spectre d'émission d'une source, qui est la température de couleur.

Depuis Planck, on sait qu'un corps noir émet un rayonnement lumineux dont le spectre dépend de la température auquel on le porte. Les hautes températures donnent un spectre tirant sur le bleu, alors que les basses températures ont un spectre tirant sur le rouge (et les températures encore plus basses tirent sur l'infrarouge).

La fonction définissant la densité d'énergie spectrale du rayonnement d'un corps noir est donné par la loi de Wien-Planck: $$ I(\lambda,T)= \frac{2 \hbar c^2}{\lambda^5} e^{-\frac{\hbar c}{\lambda k T}} $$ où $c=2.99792458\,10^8\ m/s$ est la vitesse de la lumière, $\hbar=6.62606896\,10^{-34}\ J.s$ est la constante de Planck et $k=1.3806504\,10^{-23} J/K$ est la constante de Boltzman (m: mètre, s:seconde, J:Joule, K: Kelvin, sr: stéradian). Il s'agit d'une radiance spectrale, qui s'exprime en W/m²/sr/m.
En l'intégrant sur tout le spectre, on retombe sur une quantité en W/(m². sr), qui est simplement la radiance de la source. Il existe plusieurs variantes de cette formule, qui diffèrent généralement d'un facteur $\pi$, lié au champ de vision de la source.

On peut voir ci-dessous la représentation de l'énergie spectrale pour un corps noir à une température de 5000K et pour un corps noir à 6500K (λ est en nanomètres).

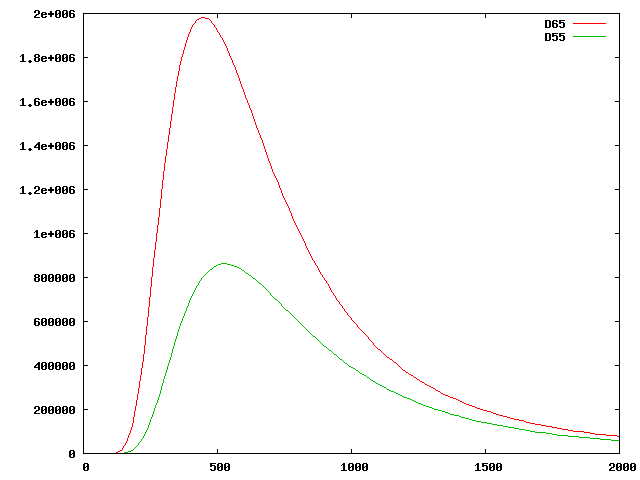
La température de couleur est un moyen commode de désigner le spectre d'une source émissive; dans le système sRGB, le spectre de l'illuminant D65 défini par la CIE peut-être approché par le spectre d'un corps noir porté à une température de 6504K (d'où le nom de D65). Si l'on mesure les coordonnées de chrominance associée au corps noir porté à la température de 6500K, on retrouvera les coordonnées du point blanc du système sRGB avec une très grande précision. Regardons plus en détail la représentation comparé du spectre de l'illuminant CIE D65 et du corps noir à 6500K:

Rappelons que le spectre visible se situe entre 400 et 750nm. On constate un net écart dans les bleus entre la radiance du corps noir et celle de l'illuminant D65 défini par la CIE. Cet écart correspond aux différences d'absorption de l'atmosphère, mais a peu d'importance en raison de la faible sensibilité de l'oeil dans le bleu.

Lorsque l'on dispose d'une source lumineuse, la température de couleur corrélée est la température du corps noir dont le spectre se rapproche le plus de celui de la source. Il n'est pas simple de définir la notion d'écart de couleur et nous y reviendrons plus loin.

Si votre moniteur est équipé d'un système de réglage de la température de couleur, vous pouvez régler différemment le blanc de référence. Une température de 6500K correspond au standard sRGB, 5000K (illuminant D₅₀) correspond plutôt à un éclairage de type tungstène, alors que 9300K (qui tire sur le bleu) a longtemps été la valeur de référence des tubes cathodiques qui, pour des raisons physiques, avaient des phosphores qui généraient plus facilement du bleu que du vert ou du rouge.

On peut voir sur le schéma suivant une représentation approximative des températures de couleur.

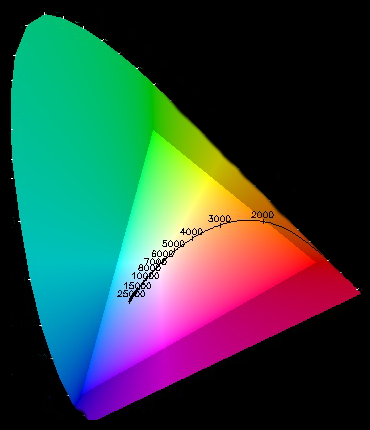
Rappelons que si votre moniteur admet un mode "sRGB", vous ne pourrez pas modifier la température de couleur en mode "sRGB", car elle est définie par la norme "sRGB" comme étant égale à l'illuminant D₆₅.

Luminosité, luminance et fonction gamma

Nous avons vu que la CIE définit la luminance comme étant: $$ Y = 0.212671 R + 0.715160 G + 0.072169 B$$ avec R, G et B exprimé dans le modèle RGB-Rec709.

Malheureusement, la luminance Y n'est pas en rapport avec le fonctionnement perceptif de l'oeil. En effet, un doublement de la valeur de Y n'aboutit pas à un doublement de la sensation de luminosité. En fait, une loi (strictement expérimentale) connue sous le nom de loi de Weber-Fechner dit que la sensibilité de l'oeil pour un niveau de luminance donné est du type: $$ \frac{\mathrm{d}\!L}{L} = 0.01 $$ Autrement dit, la capacité de l'oeil a distinguer deux niveaux différents dépend de la luminance courante, et deux niveaux, pour être distincts, doivent différer d'au moins 1%.

La loi gouvernant la sensation de luminosité n'est donc absolument pas linéaire. Le modèle CIELab dont nous avons déjà parlé à pour but de définir la luminosité $L^*$ de façon à ce qu'une augmentation de 1% de L* corresponde effectivement à une différence de 1% dans la sensation de luminosité. Rappelons que la valeur de L* est calculée de la façon suivante: $$ L^* = \begin{cases} 116 \sqrt[3]{\frac{Y}{Y_n}}-16\ \text{si}\ \frac{Y}{Y_n}\gt0.008856\\ 903.3 \frac{Y}{Y_n}\ \text{sinon} \end{cases} $$ La valeur de L* en fonction de Y est donc:

On constate que la sensibilité à la variation de $Y$ est très forte en début de courbe (dans les tons sombres), et qu'elle devient faible dans les tons clairs.

$L^*$ varie de 0 à 100, et la variation de une unité correspond en principe à la limite du perceptible pour la vision humaine. Certains auteurs (tel Norman Koren) semblent penser que l'oeil pourrait distinguer jusqu'à 200 nuances (0.5%) de luminosité. En ce qui me concerne, j'ai bien du mal, même sur du matériel haut de gamme , à atteindre 1%. Les diagrammes suivants vous aideront à vous faire une idée par vous-même.

Dans mon cas personnel, sur un moniteur haut de gamme calibré en sRGB, Une différence de 1% dans le vert est difficilement visible, elle est extrêmement difficile à voir dans le rouge (j'y parviens en déplaçant lentement la tête), et elle est, toujours pour moi, invisible dans le bleu.

Une différence de 2% est nettement visible dans le vert, et légèrement visible dans le rouge et le bleu (toujours dans mon cas personnel).

En revanche, une différence de 1/256 est virtuellement indécelable, même dans le vert:

Il faut cependant savoir que ces résultats sont largement dépendants de l'écran utilisé. Ainsi, sur l'écran de mon portable, je parviens même à distinguer le 1/256ème de nuance de vert...

Il faut maintenant signaler un fait à la fois curieux et utile; les moniteurs vidéo à tube cathodique (moniteurs CRT) avaient une loi de réponse au signal d'entrée qui était de la forme $x^\gamma$, avec $\gamma$ entre 2 et 2.7. Cette loi est purement physique et tient au fonctionnement du système cathode/anode.

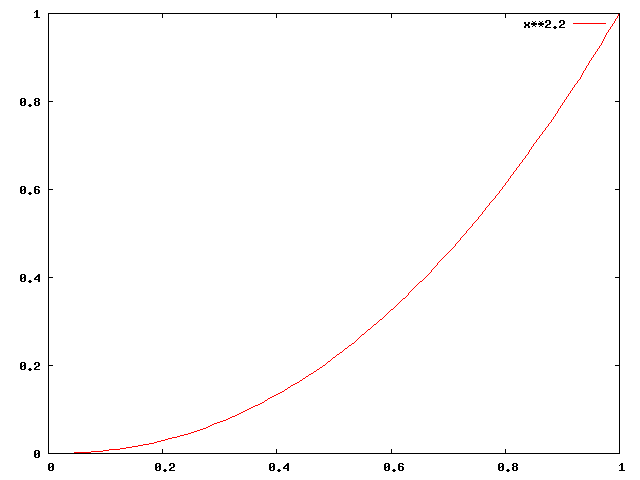
Il fallait donc normaliser le signal de sortie des équipements vidéo de façon à rendre simple l'affichage du signal sur un moniteur cathodique. La CIE dans la recommandation 709 définit ainsi des niveaux R', G' et B' qui auront la forme: $$ R'= \begin{cases} 4.5 R\ \text{pour}\ R \lt 0.018 \\ 1.099 R^{0.45} - 0.099\ \text{sinon} \end{cases} $$ La partie linéaire de la fonction dans le premier segment permet de réduire les effets du bruit liés au capteurs numériques. Cette fonction à la forme suivante:

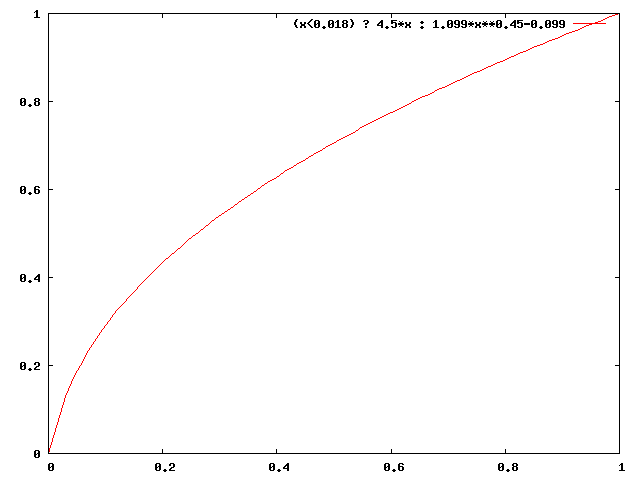
Cette transformation a pour avantage d'inverser la transformation en $x^\gamma$ pour $\gamma=2.2$. Ainsi, le signal $R'$, $G'$, $B'$ sortant d'une caméra vidéo pourra directement être injecté sur un moniteur de type CRT; l'image reconstituée sera exactement l'image d'origine.

Par chance, par hasard, ou peut-être simplement parce qu'il s'agit d'une loi physique, la loi de fonctionnement d'un moniteur CRT est exactement la loi duale de la vision humaine, et la fonction de transformation RGB → R'G'B' mimique de façon étonnante la loi de sensibilité de la vision humaine.

Le codage en R'G'B' a ainsi un autre avantage: il permet de mieux discriminer les signaux les plus importants pour l'oeil humain (dans les zones sombres) en les amplifiant. Cela aura une importance toute particulière lorsque nous devrons discrétiser le signal en le numérisant. Ce sujet est discuté dans le chapitre traitant des fichiers "RAW".

Il est intéressant de détailler le flux de données entre la caméra (ou l'appareil photo) et la visualisation finale sur l'écran, en supposant que l'on ne transfère que des données analogiques vers un moniteur CRT (là encore, nous reparlerons du cas particulier de la discrétisation, du codage des données numériques et des moniteurs de type LCD plus loin):

• Les valeurs $(R,G,B)$ linéaires exprimées dans l'espace colorimétrique de la caméra sont transformées dans l'espace colorimétrique souhaité qui peut-être du sRGB par exemple pour obtenir $(R_s,G_s,B_s)$ en mode sRGB.
• Ces valeurs sont transformés en $(R_s',G_s',B_s')$ par application de la fonction de transformation gamma sur les valeurs $(R_s,G_s,B_s)$.
• Ces valeurs sont transmises au moniteur.
• Si le moniteur est calibré avec un gamma de 2.2, il se contente d'injecter les valeurs $(R_s',G_s',B_s')$ dans son circuit analogique. Les valeurs correctes de luminosité sont reconstruites "magiquement" par la physique du canon à électron et du système de déviation cathode/anode.

Ce système est, à peu de chose près, celui utilisé pour la transmission de la télévision hertzienne.

Il existe également une luminance basée sur les valeurs R', G' et B'. Cette luminance est généralement appelée luma dans la littérature et vaut: $$ Y' = 0.299 R' + 0.587 G' + 0.114 B' $$ Notons que la luma n'est pas équivalente à la luminance Y CIE, et encore moins à la luminosité $L^*$. Il s'agit simplement d'une mesure utile.

Systèmes de représentation (écrans,...)

Nous allons regarder rapidement sur un exemple réel comment fonctionne la représentation des couleurs sur un système physique (écran). Voyons par exemple les distributions spectrales mesurées au spectromètre des trois phosphores d'un moniteur haut de gamme LaCie:

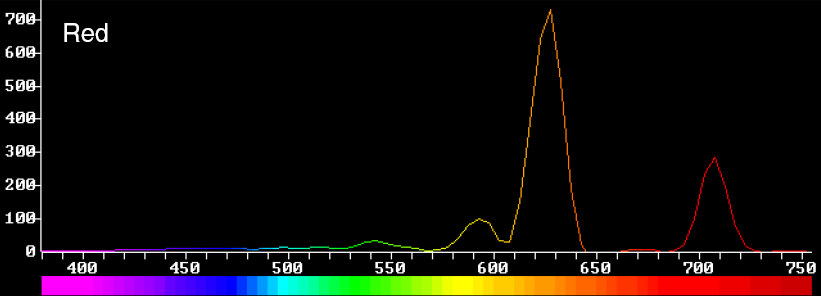
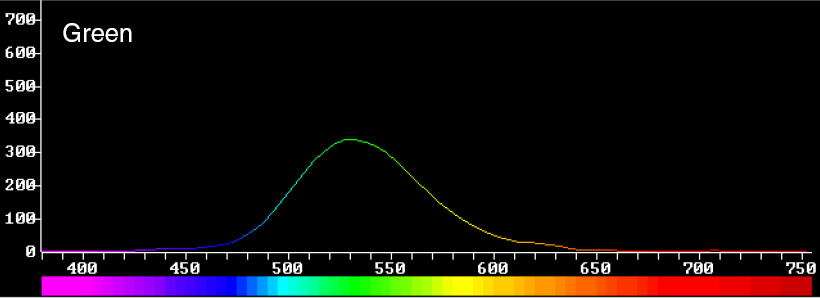
Il y a maintenant deux façons de travailler. La première est d'utiliser directement l'ensemble du gamut que l'on peut atteindre à partir de ces trois primaires (qui ne sont pas monochromatiques, mais cela n'a aucune importance). On travaille alors dans l'espace du moniteur, (ou le gamut du moniteur) directement.

Il faut bien sûr construire les matrices de passage entre ce modèle et le modèle XYZ pour respecter les représentations des couleurs. Cela se fait simplement en mesurant les coordonnées dans le système XYZ des trois primaires du moniteur à partir de leur distribution spectrale.

Il peut s'avérer utile de travailler dans le gamut du moniteur lorsque celui-ci est par exemple plus large que le gamut sRGB.

On peut aussi décider de travailler uniquement dans l'espace sRGB en restreignant le gamut du moniteur, et en le contraignant à n'afficher que des couleurs appartenant à l'espace sRGB.

Systèmes de mesure (appareils photos numériques,...)

Un appareil photo numérique se conduit comme l'oeil humain. Il dispose de trois types de capteur (que l'on peut assimiler aux trois types de cônes), qui ont des sensibilités spectrales différentes. Ainsi si nous regardons les sensibilités spectrales du capteur Kodak KAF-10500 (le capteur du Leica M8, mais équipé ici d'un filtre infrarouge...) et celles du Canon 10D:

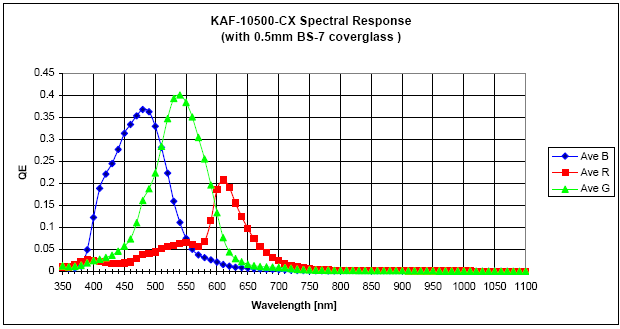
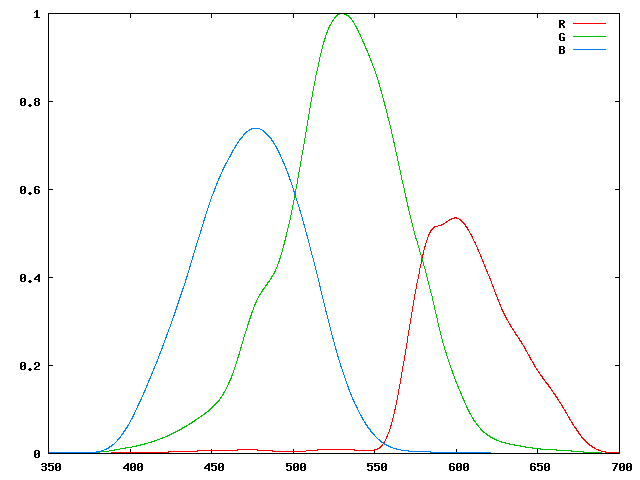
On voit que les deux capteurs ont des réponses spectrales très différentes, et que ces sensibilités sont éloignées de celles des cônes de l'oeil.

Les valeurs qui vont être obtenues en mode "RAW" en sortie de capteur ne sont évidemment pas des valeurs sRGB. Pour passer en mode sRGB, l'appareil (ou le logiciel de post-traitement), doit réaliser une conversion d'espace de coordonnées, qui ne sera qu'approchée.

En effet, le système sRGB a été construit par une transformation linéaire du modèle des cônes de l'oeil humain. En revanche, le système de capteurs de l'appareil photographique n'a aucune raison a priori de pouvoir se "mapper" de façon linéaire sur l'espace sRGB (rappelons que tous les espaces LMS, RGB-1931, sRGB, AdobeRGB sont tous déduits les uns des autres par des transformations linéaires). On peut choisir plusieurs façons de réaliser cette conversion, sans qu'il y en ait une qui soit "meilleure" qu'une autre (cela dépend du critère que l'on souhaite optimiser au moment de la conversion). Ce point est discuté plus en détail dans la suite de cet article. On peut cependant retenir deux choses de ce phénomène:

• La plupart des logiciels de conversion des "RAW" proposent une conversion vers sRGB ET vers AdobeRGB. Cela se justifie justement parce que le capteur de l'appareil, comme l'oeil, mesure le rayonnement sur l'ensemble du spectre. En utilisant AdobeRGB, il est possible de conserver des "couleurs" qui seraient perdues en sRGB au moment de la troncature des valeurs négatives des coordonnées (en effet, les espaces LMS, XYZ, RGB-1931, sRGB, AdobeRGB, est... sont équivalents puisque l'on passe de l'un à l'autre par transformation linéaire, mais cette équivalence disparaît lorsque l'on réalise la troncature des coordonnées négatives dans un espace particulier.).
• On comprend mieux pourquoi ces mêmes logiciels proposent souvent plusieurs options de conversion aux noms bizarres ("Neutre", "Fidèle" dans Canon DPP par exemple)... Il s'agit de différentes méthodes de conversion mappant le RAW sur le sRGB (ou l'AdobeRGB).

Plutôt que de réaliser une conversion vers l'espace sRGB ou AdobeRGB, nous allons chercher une conversion vers l'espace XYZ. Les conversions vers sRGB et AdobeRGB s'en déduisent immédiatement par une simple transformation matricielle.

Une méthode classique pour transformer l'espace capteur vers l'espace XYZ consiste à trouver une transformation linéaire matricielle M de la forme: $$ \begin{bmatrix} x_c(\lambda)\\ y_c(\lambda)\\ z_c(\lambda) \end{bmatrix} = \begin{bmatrix} \alpha_{11}&\alpha_{12}&\alpha_{13}\\ \alpha_{21}&\alpha_{22}&\alpha_{23}\\ \alpha_{31}&\alpha_{32}&\alpha_{33} \end{bmatrix} \begin{bmatrix} c_r(\lambda)\\ c_g(\lambda)\\ c_b(\lambda) \end{bmatrix} $$ Ici, cr, cb et cg représentent les courbes de sensibilité spectrale du capteur de l'appareil et xc, yc et zc les fonctions dans l'espace XYZ qui doivent approcher au mieux les fonctions standards x, y et z.

Nous cherchons donc un ensemble de 9 coefficients α_ij minimisant les intégrales (qui sont indépendantes): $$ \begin{matrix} \int (x(\lambda)-x_c(\lambda))\, \mathrm{d}\lambda\\ \int (y(\lambda)-y_c(\lambda))\, \mathrm{d}\lambda\\ \int (z(\lambda)-z_c(\lambda))\, \mathrm{d}\lambda \end{matrix} $$ Le calcul n'est pas extrêmement complexe; il s'agit simplement de résoudre trois systèmes de trois équations à trois inconnues. On obtient alors les coefficients des combinaisons linéaires permettant de passer de l'espace de coordonnées de l'appareil (ici le Canon 10D) à l'espace colorimétrique XYZ. On voit ci-dessous la comparaison des courbes standards de XYZ et des courbes obtenues par combinaison linéaire:

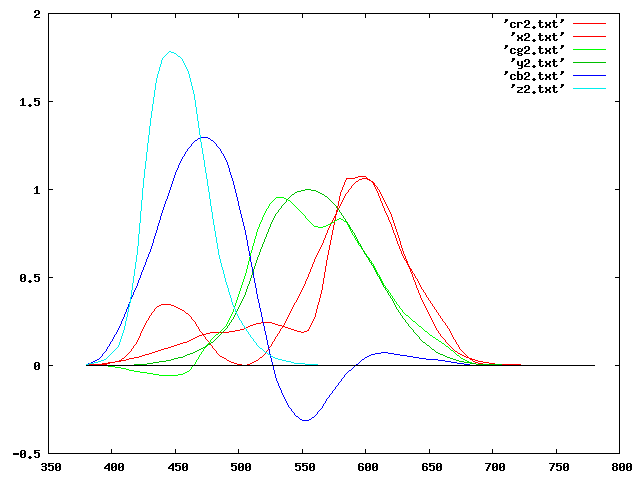
On remarque que les courbes sont relativement fidèles à partir du milieu du spectre, mais que la partie dans les faibles longueurs d'onde (vers le bleu) est moins correcte; il s'agit probablement d'un choix du constructeur, qui a préféré négliger la partie où l'oeil humain est le moins sensible, pour favoriser la zone où la sensibilité est la plus grande.

Nous avons ici obtenu les coefficients des combinaisons linéaires en faisant une minimisation suivant les moindres carrés sur les courbes XYZ; cette méthode peut être largement modulée: on peut chercher à minimiser l'écart max, plutôt que la somme des carrés des écarts, etc... Encore une fois, il existe plusieurs méthodes qui vont donner des résultats différents, sans qu'il soit possible d'en désigner une qui soit "supérieure" aux autres.

Les profils ICC

La méthode très simple décrite ci-dessus est donc insuffisante, comme nous venons de le voir. En fait, les conversions entre profils colorimétriques sont faites en utilisant les profils ICC (pour International Color Consortium target="_blank"). On trouvera ici le détail des spécifications ICC.

Les transformations ICC sont plus riches que de simples transformations matricielles. Il existe cinq transformations différentes pour passer de l'espace du système de capture à l'espace XYZ ou Lab:

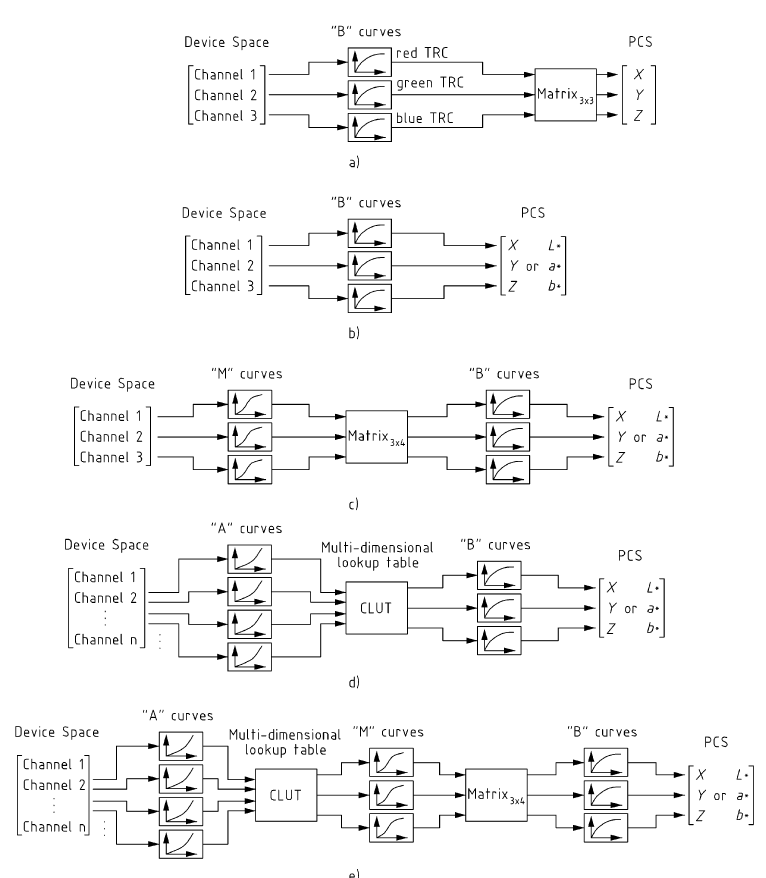
Ces modèles impliquent à la fois des transformations matricielles et des courbes de transfert.

En fait, comme dit plus haut, il est commun que les fabriquants d'appareils fournissent plusieurs profils colorimétriques différents. En théorie de la couleur, l'opération que nous venons de décrire (qui consiste à transformer une scène en image) s'appelle le rendu. Les fabricants d'appareil ne s'intéressent pas nécessairement à la fidélité du résultat. En effet, toute photographie doit être inévitablement affichée ou imprimée à un moment ou à un autre, et, dans la majorité des cas, une image rendue de façon fidèle n'est pas nécessairement très agréable à regarder (elle apparait souvent "plate"). Le consortium ICC propose de bien séparer ces deux objectifs; lorsque l'on transforme un fichier RAW de façon à rendre de façon aussi fidèle que possible la scène, on parle de rendu "Scene-Referred"; lorsque l'on veut la rendre de façon adaptée au périphérique de sortie, on parle d'image "Output Referred".

Le consortium ICC suggère d'utiliser des profils colorimétriques différents pour ces deux types de rendu. En particulier, pour les "Scene Referred", il suggère l'emploi du profil linear_RIMM-RGB comme profil ICC de sortie de votre convertisseur RAW (comme son nom l'indique, ce profil est linéaire, c'est à dire que l'image est stockée sans appliquer aucun gamma, comme l'image sortie du capteur). La méthode de conversion est alors la suivante si l'on prend comme exemple Adobe Camera Raw comme convertisseur:

• Ouvrir le fichier RAW avec ACR, et adapter les différents paramètres de la façon suivante:
  • Balance des blancs, température de couleur et teinte: adapter de façon à se rapprocher le plus possible de la scène d'origine. SI la température de couleur est connue (flash), la fixer.
  • Exposition: laisser sur 0
  • Ombres: modifier le moins possible.
  • Contraste, luminosité, saturation: laisser sur 0. Il s'agit de réglages destinés à modifier la couleur qui ne doivent pas être modifiés pour une image "Scene Referred"
  • Courbe des tons: mettre sur linéaire.
  • Détails/réduction du bruit: à modifier avec douceur, de façon là aussi à se rapprocher le plus possible de la scène d'origine sans trop en faire.
  • Calibration: c'est dans cette partie que l'on peut modifier de façon fine le rendu de la scène. En particulier on peut modifier la teinte dans les ombres de façon séparée de la balance des blancs. Bien entendu, il s'agit uniquement de se rapprocher au mieux de la scène d'origine, et en aucun cas de réaliser une interprétation "plaisante" de la photographie.
• Sélectionner comme espace de sortie ProPhotoRGB (ACR n'autorise que peu de profils de sortie) et une profondeur de 16bits/canal.
• Dans le menu "Edition", choisir "Convertir vers le profil..." et sélectionner linear_RIMM-RGB_v4 avec un rendu en colorimétrie relative. Ce profil colorimétrique peut être téléchargé ici; il doit être placé dans le dossier système approprié (windows/system32/spool/drivers/color sous windows) pour être accessible.
• Sauver l'image en incluant le profil colorimétrique.

Bien entendu, l'image ainsi obtenu devra être convertie dans le profil colorimétrique "Output Referred" appropriée lors de sa visualisation ou de son impression, généralement en employant un rendu perceptuel. Il existe aussi cinq transformations définis par le consortium ICC permettant de passer de l'espace XYZ ou Lab dans l'espace colorimétrique du système d'impression.

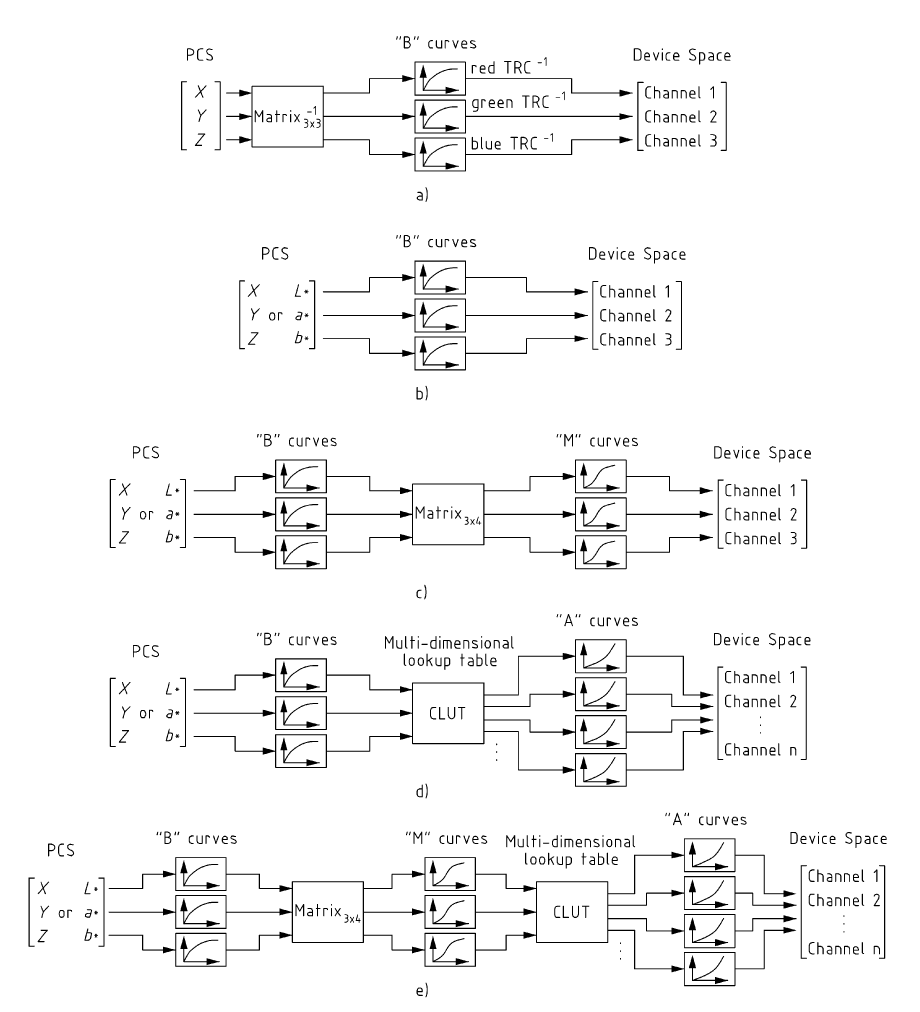
Certains sites, comme PICTO distribuent les profils ICC de leurs mini-labs. On trouve ainsi le profil ICC du minilab Fuji Frontier avec du papier Fuji Crystal. Vous pouvez ainsi charger ce profil sous Photoshop et regarder comment cela influe sur votre photographie avant de demander son impression en mode premier jet (votre fichier sera imprimé tel quel sans correction). Il est dommage que ce mécanisme ne soit pas proposé plus souvent, car il permet d'avoir un contrôle total sur la chaîne colorimétrique. Certains constructeurs d'imprimante photo fournissent également les profils colorimétriques de leur matériel (on trouvera à la fin de ce document les profils de certaines imprimantes Epson). Notons cependant que le profil ICC depend de l'imprimante et du papier utilisé.

Histogramme neutre et ETTR (Exposing To The Right)

Un dernier point pour conclure: lorsque l'on prend une photographie avec un appareil numérique, l'écran affiche un histogramme détaillé montrant les niveaux des trois canaux Rouge, Vert et Bleu. Il faut cependant savoir que ces trois histogrammes ne représentent pas les niveaux capturés par les trois types de capteur de la mosaique Bayer, mais les niveaux de Rouge, de Vert et de Bleu obtenus après conversion faite dans l'appareil, en appliquant la balance des blancs et l'espace colorimétrique choisis par l'utilisateur. Cet histogramme représente exactement les niveaux correspondant à l'image réduite qui est affichée sur l'écran de l'appareil, image qui est donc une image convertie à partir de la balance des blancs et du modèle colorimétrique. On peut voir ci-dessous l'affichage de l'écran arrière avec un équilibrage "parfait" de la balance des blancs au sens colorimétrique.

Cela peut avoir des effets néfastes; en particulier, on peut avoir l'impression sur l'histogramme qu'un canal est saturé, alors qu'il s'agit simplement de l'effet de la conversion du RAW vers le RGB: le canal R peut, par exemple, sembler proche de la saturation dans la photographie ci-dessus, alors que le véritable niveau du capteur "rouge" de la mosaique Bayer n'est pas saturé. Le phénomène inverse peut d'ailleurs aussi se produire, avec un canal "RAW" vert qui semble ici raisonnablement saturé.
Il est possible d'avoir un affichage des histogrammes qui se rapproche plus fidèlement de la valeur des trois canaux du capteur. Sur les appareils de type Canon, il suffit de faire une photo "noire" et de prendre une balance des blancs customisée définie à partir de cette photo (il existe des méthodes comme la technique "uniwb" qui permet d'atteindre le même résultat sur d'autres types d'appareil). L'inconvénient de ce procédé est que les photographies qui seront affichées sur l'écran de l'appareil présenteront une forte dominante verdatre. En effet, la représentation se calque fidèlement sur les valeurs mesurés par les trois canaux RAW, et le canal centré dans le vert ayant une plus forte amplitude que les autres, il impose sa dominante. On peut voir ci-dessous la même photographie avec cet équilibrage des blancs.

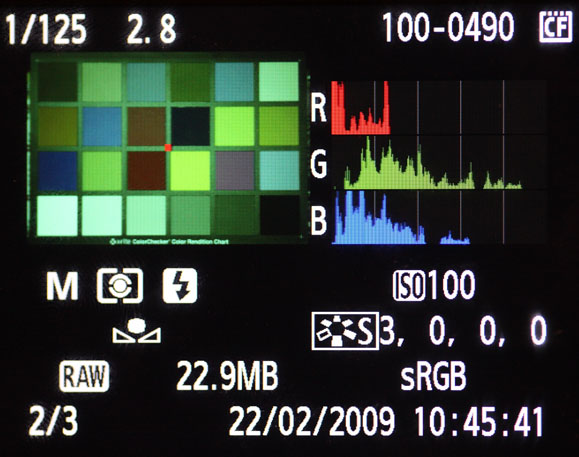
On constate qu'en fait le canal rouge est très loin de la saturation, alors que le vert en est beaucoup plus proche qu'on ne pouvait le croire dans l'histogramme initial. On voit également que la dominante verte rend l'image affichée inutilisable en terme de rendu colorimétrique...

Ce mode d'affichage des histogrammes est particulièrement utile lorsque l'on utilise une technique connue sous le nom de ETTR pour prendre ses photos, ou Exposing To The Right. L'idée derrière cette technique est qu'il faut utiliser au maximum la dynamique disponible dans le capteur, et donc caler au maximum l'histogramme sur la droite lorsque l'on prend la photo mais surtout SANS surexposer. En effet, dans le domaine de la photographie numérique, la surexposition est encore plus grave qu'en argentique. En effet, un film argentique, même surexposé, ne "coupe" pas brutalement la dynamique; il la compresse davantage. Un capteur au contraire va simplement être saturé, et toute la dynamique est totalement" coupée". La technique ETTR doit donc être utilisée avec prudence, et nécessite d'avoir une représentation absolument exacte des histogrammes de chaque canal.

Calibration de la chaîne colorimétrique

En toute logique, la notion de modèle colorimétrique devrait permettre de simplifier le travail de l'amateur, et même du professionnel. Si nous utilisons un système respectant les normes définies par l'ICC du début à la fin de la chaîne colorimétrique, les couleurs rendus à l'impression devraient être, en théorie, fidèles à celles du modèle.

Il n'en est malheureusement pas ainsi pour toutes sortes de raisons, dont certaines ont déjà été exposées dans les paragraphes précédents: difficulté technique à "mapper" au sens physique du terme les phosphores des écrans sur le sRGB, efficacité des filtres sur les micro-lentilles des capteurs d'appareil photo qui ne permettent pas là non plus un mapping direct entre les deux modèles colorimétriques au sens strict, etc, etc.

Mais tous ces problèmes physiques (et impossibles à supprimer totalement) mis à part, le problème de la calibration (que l'on appelle généralement réglage de la balance des blancs lorsqu'il s'agit du calibrage d'une photographie) de la chaîne se pose à chacun des étages de celle-ci, même avec des appareils d'excellente qualité.

La prise de vue

En principe, les appareils photographiques sont calibrés pour qu'une photographie prise avec un illuminant D65 respecte le standard colorimétrique choisi (généralement sRGB, ou pour certains appareils haut de gamme AdobeRGB). Dans ce cas, les couleurs seront reproduites de façon fidèle, aux problèmes physiques susmentionnés près.
Mais, au moment de la prise de vue, il est bien rare que l'illuminant utilisé soit un illuminant D65 standard, à l'exception du travail en studio... Il est au contraire plus que fréquent que l'on soit amené à travailler avec des lumières au tungstène en intérieur (illuminant beaucoup plus chaud).
On souhaite en général retrouver une teinte plus normale, surtout dans le cadre de photographies prises en lumière artificielle. En effet, le cerveau humain est extrêmement efficace pour gommer les différences d'illuminant, mais celles-ci seront criantes lors du visionnage de la photographie.
Notons cependant, avant d'aller plus loin, que l'on ne souhaite pas toujours retrouver exactement la couleur sRGB/D65 d'un objet. Ainsi, un coucher de soleil donne de jolis teintes jaunes orangés qui font souvent tout le charme de la photo; il n'est pas inutile de se rappeler que l'art de la photographie est aussi l'art de l'interprétation de l'image, et pas seulement de sa reproduction fidèle.

Pour rééquilibrer les couleurs au sein d'une photographie, les appareils numériques disposent de différents systèmes leur permettant d'estimer une balance des blancs probable. Il ne faut cependant se faire aucune illusion: ces systèmes automatiques ne sont pas fiables à 100%, et l'on a bien souvent des surprises au visionnage. En effet, l'appareil fait son estimation en fonction des données dont il dispose et les résultats sont souvent discutables...

On peut voir ci-dessous deux photographies prises dans les mêmes conditions d'éclairement mais avec un arrière-plan différent.

Sur la première photographie, l'arrière-plan comprend une partie bleu (le sweat shirt) qui permet à l'appareil de disposer sur l'ensemble de la photographie d'une gamme de couleurs assez étendue car le bleu complémente bien l'arrière plan rouge; le système automatique de balance des blancs peut ainsi réaliser à peu près correctement son équilibrage des couleurs.
Sur la seconde photographie, l'arrière-plan est uniquement en teintes rouges-orangés, et l'appareil corrige incorrectement la photographie vers le bleu, donnant un teint blafard.
On peut voir ci-dessous les deux photographies correctement corrigées au niveau de la balance des blancs; la première n'est quasiment pas modifiée, la seconde est totalement différente (et bien plus agréable à regarder).

Dans le cas présent le rééquilibrage a été facile car la photographie a été prise au flash (avec un réflecteur blanc) en mode RAW; les informations brutes "sorties de capteur" sont donc disponibles, et tous les logiciels de conversion connaissent la température de couleur d'un flash pro correctement équilibré.
De la même façon, ces logiciels disposent d'un ensemble de températures prédéfinies (nuageux, lumière du jour, lumière fluorescente, ombre, etc..) qui permettent d'adapter de façon semi-automatique la balance des blancs en post-traitement.
Réaliser la même opération sur une photographie prise en mode JPEG demande plus de soin. En effet, il faut penser à régler la balance des blancs soi-même sur l'appareil au moment où l'on va prendre la photographie. Les appareils disposent aussi en général de plusieurs pré-réglages par défaut de même type que les logiciels de post-traitement des RAWs. Cependant, en mode JPEG, la conversion est effectuée dans l'appareil, et les informations "brut de capteur" sont perdues, rendant les post-traitements bien compliqués. D'autre part, l'on a souvent trop tendance à "oublier" de régler la balance des blancs, et à faire (souvent bien à tort) confiance au système automatique de l'appareil; en mode JPEG, la récupération a posteriori est bien plus difficile.

Rappelons en effet qu'en mode RAW, l'information stockée ne dépend pas de la température de couleur définie par l'appareil: on se contente de stocker les informations de coordonnées colorimétriques mesurées suivant les courbes de réponse spectrale de l'appareil; elles ne subissent aucune pondération. C'est au visionnage que le logiciel de conversion RAW réalise la conversion vers l'espace colorimétrique (sRGB ou AdobeRGB) et réalise aussi la transformation liée au spectre émissif supposé de la source lumineuse.

Il est également possible de réaliser des balances des blancs manuelles très fines en utilisant des chartes de Munsell. Nous en reparlerons plus loin.

Le calibrage d'un écran

Certains écrans sont supposés être calibrés "par défaut" en mode sRGB. Il n'est cependant pas inutile de vérifier ce calibrage "par défaut", voire de le modifier dans certains cas.

Il existe plusieurs méthodes de calibrage. La plus simple, la plus efficace mais aussi la plus onéreuse est d'utiliser une sonde de couleur avec le logiciel adapté. Il s'agit d'un système de mesure de luminance qui se pose sur l'écran et se raccorde à votre ordinateur grâce au port USB. Un logiciel spécialisé compare les luminances mesurées par la sonde aux valeurs des pixels qu'il affiche simultanément sur l'écran: le logiciel affiche successivement plusieurs intensités de rouge, puis de vert, puis de bleu. A partir de ces mesures, il construit un profil colorimétrique (ou profil ICC) de l'écran qui pourra être utilisé directement par windows. On peut voir ci-dessous une telle sonde en cours d'utilisation.

On peut aussi réaliser manuellement le calibrage d'un écran avec une charte de Munsell. On peut en commander en France (marque XRite) auprès de la boutique photim. Il faut noter que cette charte pourra servir par la suite à contrôler une balance de couleur, ou étalonner une imprimante, ce n'est donc pas un achat inutile...
Il faut ensuite disposer d'une charte de Munsell en format électronique comme celle-ci.

Si vous souhaitez avoir un profil absolument exact, vous pouvez télécharger cette image au format tif en mode Lab. Elle correspond exactement à la charte XRite. Elle a été fabriquée en fonction des profils fournis par X-rite: X-rite fournit en effet avec sa charte une table donnant pour chacune des 24 couleurs les composantes exactes dans l'espace Lab et dans l'espace sRGB. Il s'agit d'un fichier tif avec un profil ICC sRGB,
Voici la table des valeurs décrite de gauche à droite et de haut en bas:

115, 82, 68	194, 150, 130	98, 122, 157	87, 108, 67	133, 128, 177	103, 189, 170
214, 126, 44	80, 91, 166	193, 90, 99	94, 60, 108	157, 188, 64	224, 163, 46
56, 61, 150	70, 148, 73	175, 54, 60	231, 199, 31	187, 86, 149	8, 133, 161
243, 243, 242	200, 200, 200	160, 160, 160	122, 122, 121	85, 85, 85	52, 52, 52

Il faut cependant faire attention: il existe plusieurs types de charte, et elles ne présentent pas toutes les mêmes couleurs! Ainsi la charte GretagMacbeth (qui est examinée dans le détail sur le site de Bruce Lindblom) n'a pas exactement les mêmes couleurs que la charte X-Rite.

Pour calibrer votre moniteur, il faut pousser au maximum la luminosité de votre écran, et régler le contraste sur 50%. Ensuite, il faut modifier les paramètres de conversion de couleur, ce qui peut se faire simplement à partir des logiciels de contrôle de la carte graphique (le catalyst center d'ATI ou le panneau de configuration nvidia), en essayant de faire en sorte que les couleurs affichées sur l'écran correspondent à celle de la charte. Il faut cependant bien faire attention: en fonction de l'éclairage ambiant de la pièce, les couleurs de la charte "papier" seront différentes. Idéalement, il faudrait l'éclairer avec une lampe donnant une illumination standard. A défaut, la lumière du jour peut convenir.

Par cette méthode, on peut arriver à faible coût à réaliser un calibrage correct pour un écran quelconque.

Utilisation des chartes de Munsell pour le réglage de la balance des blancs

Il est également possible de réaliser une balance des blancs extrêmement fine (et totalement manuelle), en photographiant une charte de Munsell, et en s'assurant que les photographies suivantes seront prises dans les mêmes conditions d'éclairement. Lors du post-traitement, il faudra charger la photographie de la charte de Munsell, et équilibrer les couleurs à l'aide d'un logiciel de traitement d'image. Cette méthode peut aussi être appliquée à un scanner.
Cela peut se faire de plusieurs façons: soit visuellement, en comparant la charte "papier" et la photographie (mais il faut être certain que l'écran est parfaitement calibré), soit en vérifiant les valeurs RGB de chacun des carrés de la charte.
Une fois que l'on a trouvé la modification idoine de l'équilibre des couleurs sur la charte, il suffira de le noter puis de l'appliquer à chacune des photographies de la prise de vue.

On peut voir dans l'exemple ci-dessous l'opération d'équilibrage appliquée à un scan d'une charte de Munsell. A gauche, la charte de référence, au centre la charte scannée sans correction et à droite, la charte scannée après correction.

Il a fallu diminuer le contraste et augmenter la luminosité pour obtenir un résultat de bien meilleure qualité. Ce n'est certes pas parfait, mais l'on est beaucoup plus proche de l'original

Comparaison de la qualité de conversion colorimétrique

Il est parfois aussi intéressant de comparer différents appareils et de voir comment les capteurs réagissent, et comment les logiciels de conversion passent de l'espace colorimétrique de l'appareil à l'espace sRGB. On trouve ci-dessous la mire munsell standard en haut à gauche suivi (de gauche à droite puis de haut en bas) de celle obtenue avec un Canon 1Ds MarkII, un Epson RD-1 et un Nikon Coolpix 8400.
Ces photographies ont été prises exactement dans les mêmes conditions d'éclairement et le développement numérique a été fait par le même logiciel, en forçant la même température de couleur (qui était connue).

Les conversions ne sont pas parfaites, et nous pouvions nous en douter depuis que nous avions constaté que les courbes de sensibilité spectrale des appareils ne pouvaient pas se "mapper" de façon parfaite sur un modèle colorimétrique sRGB.

Importance de la luminosité ambiante

Il est inutile de calibrer finement la chaine de visualisation si l'environnement dans lequel on regarde les objets n'est pas lui-même relativement neutre. Un des exemples les plus classiques est le suivant:

Les faces unitaires pointées sur chacun des deux cubes émettent exactement le même type de rayonnement: elles sont gris médian (autant de rouge que de vert et de bleu). Pour vous en convaincre vous pouvez télécharger l'image sous photoshop ou gimp et mesurer la valeur de la couleur de chacune des faces avec l'outil pipette. Pourtant, la face apparait bleu dans un environnement jaune (à gauche) et jaune dans un environnement bleu (à droite).

Ressources en ligne

Draft du standard sRGB
Conversion entre espaces de couleurs
Tout sur le gamma
Beaucoup de choses sur la couleur
Le modèle CIE LAB
Reference Input/Output Medium Metric RGB
Profil ProPhotoRGB pour windows
Profil ICC sRGB v4
Profil ICC ROMM ISO22028
Profil ICC linear RIMM RGB v4
Profil pour DCRAW avec Gamma=1 sRGB
Profil pour DCRAW avec Gamma=1 AdobeRGB
Profils pour imprimantes Epson réalisés par PixelGenius
Specification ICC.1:2004-10
ICC Profile Inspector

---

Retour à la page d'accueil.

Le téléchargement ou la reproduction des documents et photographies présents sur ce site sont autorisés à condition que leur origine soit explicitement mentionnée et que leur utilisation se limite à des fins non commerciales, notamment de recherche, d'éducation et d'enseignement.
Tous droits réservés.

Dernière modification: 17:42, 24/06/2024