
Radiométrie et photométrie
Radiométrie
La radiométrie s'intéresse à la quantification de l'énergie émise ou incidente sur une surface.
Définition de l'angle solide
Un angle plat est défini comme étant le rapport de la longueur de l'arc qu'il définit sur le cercle par le rayon du cercle. De la même façon, un angle solide est défini comme le rapport de la surface interceptée divisée par le rayon de la sphère élevé au carré, soit $\Omega = \frac{A}{R^2}$
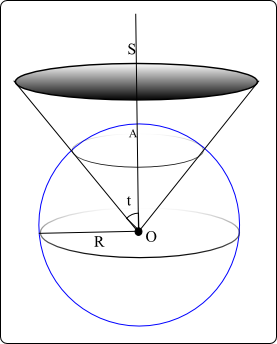
Il est facile de démontrer dans le cas d'une calotte sphérique que
l'angle solide est indépendant du rayon de la sphère de référence. En
effet, dans le cas de la figure ci-dessus, la surface
$A = 2 \pi R^2 \, \left(1 - \cos(t)\right)$.
L'angle solide vaut donc
$\Omega=2\pi \left(1-\cos(t)\right)$.
On remarque que pour $t = \pi$ (la sphère complète)
l'angle solide $\Omega$ vaut $4 \pi$. Il faut cependant noter que la forme de la
surface interceptée peut-être quelconque dans le cas général, ce qui
ne change en rien le résultat.
L'unité employée pour les angles solides est le stéradian,
dont l'abbréviation est st.
L'angle solide permet de mesurer une partie du champ visuel de
l'observateur.
On peut citer, comme exemple d'angle solide, l'angle suivant lequel on
voit le soleil depuis la terre, qui est de 0.00006 st. Celui suivant
lequel on voit la lune est le même; ce qui explique que, lors d'une
éclipse, les deux disques se recouvrent presque parfaitement, ce qui
permet à la lune de cacher le soleil tout en laissant visible au
télescope certains éléments de la couronne solaire.
Flux énergétique
Le flux énergétique (ou puissance optique) est la puissance totale du
rayonnement émis par une source lumineuse. Cette puissance est mesurée
en Watts. Il s'agit d'une mesure qui ne fait intervenir ni
distribution spectrale du rayonnement, ni distribution spatiale. Le
rayonnement peut être aussi bien isotrope (la source émet de façon
uniforme dans toutes les directions) qu'anisotrope. On note
généralement le flux énergétique
$\Phi_e$.
L'efficacité d'une lampe mesure en général le rapport de la
puissance consommée par rapport au flux énergétique restitué dans
le spectre visible. Pour une lampe traditionnelle (filament
incandescent), la
puissance consommée par la lampe correspond à la totalité de l'énergie
dissipée, ce qui inclut un flux énergétique émis des très grandes
longueurs d'ondes (infra-rouges et au delà) jusqu'au spectre
visible. Ces lampes sont peu efficaces, car elles diffusent une grande
partie de leur puissance radiative hors du spectre visible. Les lampes
à économie d'énergie, qui fonctionnent sur le principe des tubes
fluorescents (voir ce
chapitre), sont
beaucoup plus efficaces.
Intensité énergétique
L'intensité énergétique $I_e$ décrit la distribution spatiale du rayonnement d'une source. On a donc:
$$ \mathrm{d}\Phi_e=I_e \mathrm{d}\Omega$$Le flux énergétique s'obtient en intégrant $I_e \mathrm{d}\Omega$ sur l'ensemble de la sphère, soit un angle solide de $4\pi$ stéradians. $$\Phi_e=\int_{4\pi} I_e \mathrm{d}\Omega$$ L'unité de l'intensité énergétique est le Watt par stéradian (W/st).
Radiance
La radiance (généralement notée $L_e$) mesure l'intensité d'un rayonnement émis à partir d'une position donnée dans une direction donnée (on appelle aussi parfois la radiance brillance).
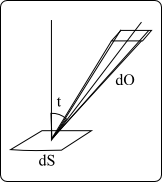
Le flux énergétique $\Phi_e$ est défini par: $$ \mathrm{d}\Phi_e = L_e \cos(t) \mathrm{d}\!S \mathrm{d}\Omega $$ De la même façon, on a: $$ \mathrm{d}I_e = L_e \cos(t) \mathrm{d}\!S $$ L'intensité énergétique $I_e$ s'obtient en intégrant cette quantité sur toute la surface emissive. $$ I_e = \int_S L_e \cos(t) \mathrm{d}\!S $$ L'unité de radiance est le Watt par mètre carré par stéradian $W/(m^2 st)$.
Exitance
L'exitance (généralement notée $M_e$) mesure le flux énergétique émis par une source à partir d'un point donné pour une surface élémentaire donné. On peut écrire: $$ \mathrm{d}\Phi_e = M_e \mathrm{d}S $$ A partir de la définition de la radiance, on voit que l'on a également: $$ \mathrm{d}M_e = L_e \cos(t) \mathrm{d}\Omega $$ L'exitance s'obtient en intégrant la quantité précédente sur l'angle solide de $2\pi$ stéradians correspondant à la demi-sphère située au dessus de la surface. $$ M_e = \int_{2\pi} L_e \cos(t) \mathrm{d}\Omega $$ L'unité d'exitance est le Watt par mètre carré $W/m^2$.
Irradiance
L'irradiance (ou éclairement énergétique) mesure le flux énergétique incident par unité de surface.
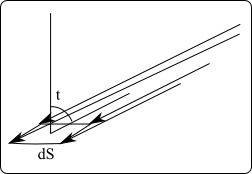
On le note généralement $E_e$. On a: $$ \mathrm{d}\Phi_e = E_e \mathrm{d}\!S $$ L'irradiance est bien sûr maximale quand la surface est orthogonale au faisceau incident. Si on note $t$ l'angle fait par la normale à la surface avec le faisceau incident, il est souvent utile de définir une grandeur $$E_{e,\mathrm{normal}} = \frac{E_e}{\cos(t)}$$
L'unité d'irradiance est le Watt par mètre carré $W/m^2$. On remarque que l'exitance et l'irradiance mesurent des quantités duales: la première est le flux énergétique emis par unité de surface, et l'autre le flux énergétique reçu par unité de surface.
Flux énergétique spectral, intensité énergétique spectrale, radiance spectrale, exitance spectrale
Les grandeurs définies ci-dessus mesurent des valeurs globales sur l'ensemble du spectre. On peut souhaiter rafiner ces grandeurs suivant leur distribution spectrale. Le flux énergétique spectral $\Phi_\lambda(\lambda)$ définit la distribution spectrale de la puissance énergétique. On a alors: $$ \mathrm{d}\Phi_e = \Phi_\lambda(\lambda) \mathrm{d}\lambda $$ Le flux énergétique total s'obtient en intégrant la quantité ci-dessus sur tout le spectre. $$ \Phi_e = \int \Phi_\lambda(\lambda) \mathrm{d}\lambda $$ L'unité de flux énergétique spectral est le Watt par nanomètre $W/nm$.
On peut de la même façon définir une intensité énergétique spectrale $I_\lambda(\lambda)$, une radiance spectrale $L_\lambda(\lambda)$, et une exitance spectrale $M_\lambda(\lambda)$.
Photométrie
Conversions et fonctions de pondération spectrale
La radiométrie mesure des quantités objectives qui sont quantifiables à partir d'instruments scientifiques de mesure, comme des spectromètres. Le problème de la photométrie est de tenter de mesurer le même type de quantité, mais en les pondérant en fonction de la sensibilité de l'oeil humain pour chaque fréquence. Le problème est complexe, d'une part parce qu'il y a une inévitable variation en fonction des sujets, mais aussi parce que la sensibilité spectrale de la vision humaine varie en fonction de l'éclairement. L'oeil humain est en effet composé de deux grands types de cellules, les cônes et les batonnets. Par faible éclairement, seuls les batonnets sont actifs, et ils permettent une vision en "noir et blanc" appelé vision scotopique.
Nous ne nous
intéresserons ici
qu'à la vision humaine en forte luminosité, lorsque ce sont les cônes
de l'oeil qui sont actifs, connue sous le nom de vision
photopique. Les cônes sont eux-mêmes divisés en trois grandes
catégories, les cônes L, M et S, qui permettent au système de vision
de construire les informations de couleur. Ce point est détaillé dans
le
chapitre consacré à la perception de la
couleur et à la colorimétrie.
La fonction de pondération spectrale est généralement notée
$V(\lambda)$ et a été
définie par la Commission Internationale de l'Eclairage (CIE) il y a
de nombreuses années. Elle a la forme suivante:
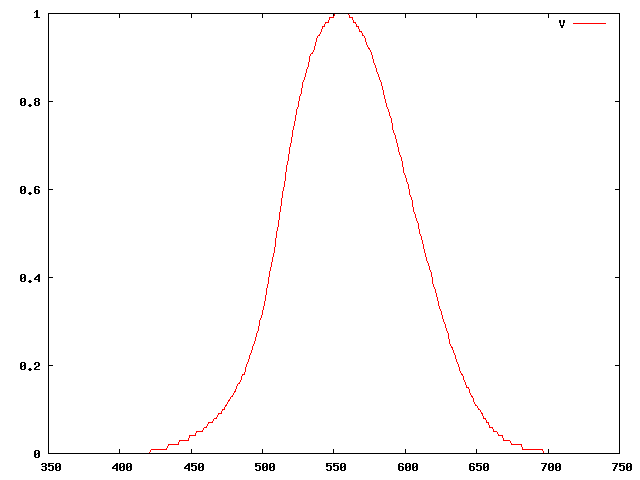
Depuis sa définition, des résultats plus récents ont montré que les valeurs de $V(\lambda)$ étaient probablement mal évaluées, en particulier dans les faibles longueurs d'onde. Cependant, $V(\lambda)$ reste la norme CIE.
Flux lumineux
Le flux lumineux correspond au flux énergétique pondéré par la courbe de sensibilité $V(\lambda)$; il est généralement noté $\Phi_v$. L'unité de flux lumineux est le lumen (lm). Une source monochromatique émettant à la longueur d'onde de 555nm un flux énergétique de 1W fournit un flux lumineux de 683 lm par définition. La quantité $K_m=683$ lm/W est une constante de conversion.
On a par définition: $$\mathrm{d}\Phi_v=K_m V(\lambda)\Phi_\lambda(\lambda)\mathrm{d}\!\lambda$$ Le flux lumineux total s'obtient en intégrant la quantité ci-dessus sur l'ensemble du spectre visible: $$\Phi_v = \int_{400}^{700} K_m V(\lambda)\Phi_\lambda(\lambda)\mathrm{d}\!\lambda$$
Intensité lumineuse
L'intensité lumineuse est le pendant photométrique de l'intensité énergétique Ie. Elle est généralement notée $I_v$. On a donc par définition: $$\mathrm{d}\Phi_v = I_v \mathrm{d}\Omega$$ Le flux lumineux s'obtient en intégrant $I_v \mathrm{d}\Omega$ sur l'ensemble de la sphère, soit un angle solide de $4\pi$ stéradians. $$\Phi_v = \int_{4\pi} I_v \mathrm{d}\Omega$$ L'unité de l'intensité lumineuse est le lumen par stéradian (lm/st), connue aussi sous le nom de candéla (cd).
Luminance
La luminance est le pendant photométrique de la radiance. On la note généralement $L_v$. Le flux lumineux total est défini par: $$\mathrm{d}\Phi_v = L_v \cos(t) \mathrm{d}\!S \mathrm{d}\Omega$$ De la même façon, on a: $$\mathrm{d}\!I_v = L_v \cos(t) \mathrm{d}\!S$$ L'intensité lumineuse Iv s'obtient en intégrant cette quantité sur toute la surface emissive. $$I_v = \int_S L_v \cos(t) \mathrm{d}\!S$$ L'unité de luminance est le lumen par mètre carré par stéradian $lm/(m^2 st)$, ou aussi le candéla par metre carré $cd/m^2$.
Exitance lumineuse
L'exitance lumineuse, généralement noté $M_v$ est le pendant photométrique de l'exitance radiométrique. On a donc: $$\mathrm{d}\Phi_v = M_v \mathrm{d}\!S$$ A partir de la définition de la luminance, on voit que l'on a également: $$\mathrm{d}M_v = L_v \cos(t) \mathrm{d}\Omega$$ L'exitance s'obtient en intégrant la quantité précédente sur l'angle solide de $2\pi$ stéradians correspondant à la demi-sphère située au dessus de la surface. $$M_v = \int_{2\pi} L_v \cos(t) \mathrm{d}\Omega$$ L'unité d'exitance est le lumen par mètre carré $lm/m^2$.
Eclairement lumineux
L'éclairement lumineux, noté $E_v$, est le pendant photométrique de l'irradiance (ou éclairement énergétique). On a: $$ \mathrm{d}\Phi_v = E_v \mathrm{d}\!S$$ L'éclairement est là aussi maximal quand la surface est orthogonale au faisceau incident.
L'unité d'éclairement est le lumen par mètre carré $lm/m^2$, comme pour l'exitance lumineuse. Mais, pour l'éclairement (et seulement l'éclairement), il est de coutume d'employer le terme de lux au lieu de $lm/m^2$.
Le téléchargement ou la reproduction des documents et photographies
présents sur ce site sont autorisés à condition que leur origine soit
explicitement mentionnée et que leur utilisation
se limite à des fins non commerciales, notamment de recherche,
d'éducation et d'enseignement.
Tous droits réservés.
Dernière modification: 21:48, 07/03/2024