headlogo2

Éléments d'optique géométrique

Lois générales de la propagation de la lumière

Domaine de l'optique géométrique

L'optique géométrique se préoccupe exclusivement des phénomènes et propriétés de la lumière qui sont hors du domaine quantique, même si la justification de certaines des lois de l'optique géométrique se trouvent dans la théorie électromagnétique et la théorie quantique.

Les lois de l'optique géométrique se sont développées lentement. La question principale posée par l'optique géométrique concerne la notion de chemin optique. Quel "trajet" suit un rayon lumineux pour aller d'un point $A$ à un point $A'$, et comment se forme l'image d'un objet à travers un système optique?

Propagation en ligne droite

A l'intérieur d'un milieu homogène, la loi de diffusion en ligne droite des rayons optiques a été connue très tôt. Elle est intuitive et a été mise en évidence en utilisant un écran perçu d'un trou laissant passer la lumière. La lumière issu de $A$ n'atteint $A'$ que lorsque le trou se trouve aligné avec $A$ et $A'$.

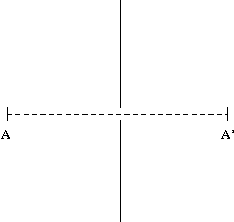
Cependant, on observe également au niveau de la fente de l'écran un phénomène curieux: la fente semble rediffuser une partie de la lumière comme si elle agissait à son tour comme une source. Nous examinerons ce phénomène, connu sous le nom de diffraction, plus tard.

Réflexion sur un miroir

La loi de la réflexion sur les miroirs a elle aussi été pressentie très tôt. Sur un miroir, le chemin suivi pour aller de $A$ à $A'$ est le chemin vérifiant la propriété $i_1=i_2$

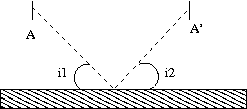
Nous ne nous intéresserons pas dans la suite de ce document aux systèmes utilisant des miroirs (connus sous le nom de systèmes catadioptriques). Ils sont plus du domaine des instruments d'astronomie, que du domaine des optiques photographiques.

Loi de la réfraction

Les lois sur la réfraction ont posé plus de problème. Il s'agit de savoir quel chemin suit un rayon qui passe d'un milieu homogène à un autre milieu homogène, les deux milieux étant différents. Un tel système s'appelle un dioptre.

L'exemple connu de tous est le problème du passage de l'air à l'eau. On voit bien que le chemin des rayons est dévié (il suffit de tremper un doigt dans l'eau et de remarquer la discontinuité à l'interface), mais la question était de savoir quelle était la loi exacte qui déterminait le trajet du rayon. Plusieurs lois ont été proposées expérimentalement. Ainsi Kepler avait établi pour le verre une loi de la forme $i_1/i_2=3/2$
Il semblerait que ce soit l'anglais Harriott qui en 1558 ait donné la loi dite des sinus, retrouvée toujours expérimentalement par le Hollandais Snell vers 1620 (mais publiée bien plus tard vers 1660) et démontrée de façon d'ailleurs incorrecte par Descartes en 1637.

La véritable fondation de l'optique géométrique est à mettre au crédit de Pierre de Fermat qui en 1658 a établi le principe de chemin extrémal: un rayon lumineux suit le trajet de temps extrémal pour aller du point $A$ au point $A'$. Cette loi permet de retrouver tous les cas connus (ligne droite dans un milieu homogène, angles égaux pour un miroir plan) et permet aussi d'établir de façon rigoureuse la loi dite des sinus. Fermat a également affirmé (de façon correcte) que la vitesse de la lumière est plus rapide dans le vide que dans les autres milieux (un problème discuté de longue date, Descartes étant de l'avis contraire). On notera désormais $n_1=c/v_1$ le rapport de la vitesse de la lumière dans le vide divisée par la vitesse de la lumière dans le milieu 1. Ce rapport est toujours supérieur à 1.

On peut comprendre cette loi de temps extrémal par une analogie simple. Supposons que vous vous trouvez sur la plage au point $A$ et qu'un baigneur est en train de se noyer au point $A'$. Quel est le chemin à suivre pour le secourir le plus rapidement possible, sachant que vous courez plus vite sur la plage que vous ne nagez dans l'eau? Le point B correspond au point où vous allez plonger dans l'eau. Si vous courez beaucoup plus vite que vous ne nagez, vous aurez intérêt à maximiser la distance parcourue sur la plage et minimiser celle parcourue dans l'eau: cela revient à mettre le point $B$ à la verticale du point $A'$. Si vous nagez aussi vite que vous courez, vous aurez intérêt à suivre la ligne droite reliant $A$ à $A'$. La position du point $B$ dépend donc bien du rapport des vitesses dans l'eau et sur le sable.

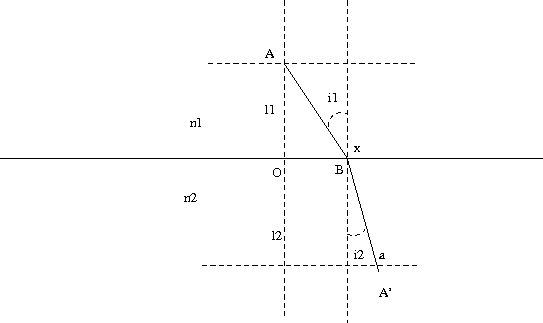
Pour établir la loi des sinus, on écrit tout d'abord le temps de parcours total qui est la somme du temps de parcours dans le milieu 1 et dans le milieu 2. On a:

$$ t= \frac{\sqrt{x^2+l_1^2}}{v_1}+\frac{\sqrt{(x-a)^2+l_2^2}}{v_2} $$

Ce temps sera extrémal quand:

$$ \def\d{\mathrm{d}} \frac{\d t}{\d x}=0$$

La résolution de cette équation est une simple question de technique sans grand intérêt et permet de montrer que le point $B$ doit se trouver à la position vérifiant:

$$ n_1 \sin(i_1)=n_2\sin(i_2)$$

Cette loi fonde totalement l'optique géométrique. Nous n'aurons besoin d'aucun autre résultat théorique que la loi des sinus.

On peut remarquer qu'il existe un angle limite $i_2=\arcsin(n_1/n_2)$
Un rayon ayant un angle d'incidence supérieur à cet angle ne peut échapper au milieu le plus réfringent (ici le milieu 2). Cette propriété est utilisé pour la transmission du signal dans les fibres optiques.

Propriétés des systèmes optiques

Image d'un point par un système optique - cas du dioptre plan

L'image d'un point par un système optique s'obtient en construisant l'intersection de tous les rayons issus du point A source. Nous allons nous intéresser ici à un exemple simple, celui d'un pécheur observant un objet au fond de l'eau. Nous avons donc affaire à un dioptre plan tel que celui représenté ci-dessous.

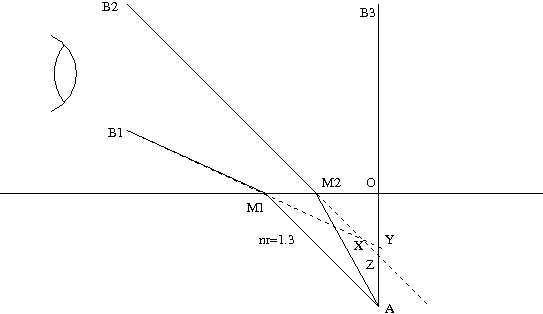
Considérons tout d'abord deux rayons issus de $A$ passant l'un par $M1$ et l'autre par $M2$. Ils sont déviés selon la loi des sinus lors de la traversée de la surface. L'oeil de l'observateur perçoit donc deux rayons $B1$ et $B2$ qui semblent provenir d'un point $X$ situé dans l'eau au point d'intersection des droites $M2B2$ et $M1B1$. Remarquons tout de suite que la position de ce point varie en fonction de la position de l'observateur. On voit en particulier que si l'on considère l'intersection des rayons $B1$ et $B3$ ou $B2$ et $B3$, les points d'intersection $Y$ et $Z$ diffèrent de $X$. Que faut-il en conclure? En fait, l'image du point $A$ est une grosse tâche. Sa perception dépend des rayons que l'oeil de l'observateur va capter. La pupille de l'oeil agit comme un diaphragme qui détermine la distance $B1B2$, et détermine la position du point d'intersection des droites. Cela explique que l'image d'un objet situé sous l'eau semble se déplacer lorsque nous nous déplaçons. Plus nous nous approchons de la verticale et plus l'image descend et s'éloigne. Plus nous adoptons un regard rasant et plus l'image avance et remonte. Remarquons également que l'objet semble toujours plus haut qu'il n'est en réalité. C'est pour cette raison qu'il nous apparaît comme étant plus gros.

Dans la mesure où les rayons issus de $A$ ne passent pas tous par le même point image $A'$, le dioptre plan est dit astigmatique . Enfin, notons que, les rayons ne passant pas tous par le même point image, l'image elle-même sera légèrement floue (et d'autant plus floue que l'on observera avec une incidence rasante).

Conditions de Gauss - cas du dioptre plan

Supposons maintenant que nous placions l'oeil de l'observateur "presque" à la verticale du point $A$ et que nous cherchions à nouveau la position du point $A'$ intersection de deux rayons issus de $A$.

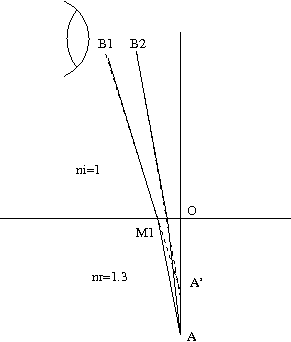
Si nous sommes près de la normale $AO$, le point $A'$ va se placer exactement sur la normale si l'on considère l'intersection des droites $M1B1$ et $AO$ ou $M2B2$ et $AO$, et très proche de la normale si on considère l'intersection des droites $M1B1$ et $M2B2$. Nous nous intéresserons donc exclusivement à chercher l'ordonnée de $A'$ sur la droite $AO$, en considérant que son abscisse est de toute façon proche de 0.

Considérons par exemple le rayon $AM1B1$. Une simple considération géométrique sur le triangle $AOM1$ nous donne:

$$\frac{OM1}{OA}=\tan(i)$$

et pour le triangle $A'OM1$:

$$\frac{OM1}{OA'}=\tan(r)$$

Soit:

$$\frac{OA'}{OA}=\frac{\tan(i)}{\tan(r)}$$

Si les angles sont petits, on peut confondre la tangente de l'angle avec l'angle lui-même. On a alors:

$$\frac{OA'}{OA}=\frac{i}{r}=\frac{1}{n_r}$$

La position du point $A'$ est donc indépendante du rayon choisi lorsque l'on se trouve proche de l'axe. Un dioptre plan, pour des rayons proches de la normale et peu inclinés, est dit stigmatique. La quantité $OA/n_r$ est appelé profondeur de l'image gaussienne. C'est ainsi par exemple qu'un objet situé à 1 mètre sous l'eau est vu comme se trouvant à environ 75cms lorsque l'on regarde à la verticale.

L'approximation de Gauss demande donc que les deux conditions suivantes soient remplies:

Notons enfin que dans le cadre de l'approximation de Gauss, le dioptre plan est stigmatique et l'image de l'objet est donc nette.

Le dioptre sphérique

Introduction

Un dioptre sphérique est un système composé de deux milieux d'indice différent dont la surface de séparation est une sphère de rayon de courbure $R$. Le dioptre plan est un cas limite du dioptre sphérique avec $R$ qui tend vers l'infini.

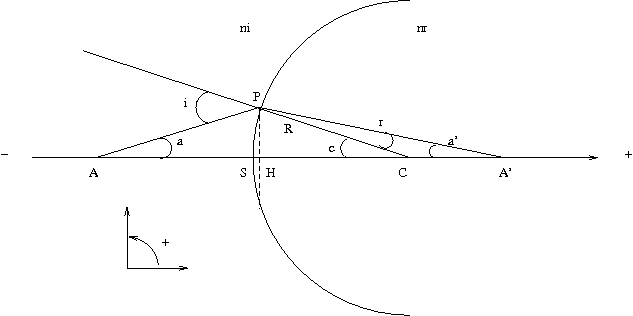
Relation de conjugaison

Nous allons établir la relation fondamentale des dioptres, connus sous le nom de relation de conjugaison, qui permet de déterminer la position $A'$ de l'image d'un point $A$ à travers le dioptre. Notons que cette relation sera établi exclusivement dans le cadre de l'approximation de Gauss.

Nous allons utiliser des quantités algébriques pour réaliser notre calcul avec l'axe du dioptre orienté vers la droite. Les angles seront mesurés dans le sens trigonométrique. Nous poserons $p=SA$ et $p'=SA'$ (dans le cadre de la figure ci-dessus, $p$ est négatif et $p'$ positif). Nous posons également $R = SC$, rayon de courbure du dioptre. Écrivons tout d'abord les relations sur les angles du triangle $PAC$:

$$a+(\pi-i)+(-c)=\pi\ \mathrm{soit}\ i=a-c$$

Pour le triangle $PCA'$:

$$(-a')+r+(\pi-(-c))=\pi\ \mathrm{soit}\ r=a'-c$$

En écrivant la relation de Snell-Descartes au point P nous avons:

\begin{align*} n_r\sin(r) &= n_i \sin(i)\\ n_r\sin(a'-c)&=n_i\sin(a-c) \end{align*}

Les angles étant petits, on peut remplacer le sinus par l'angle lui-même, et l'on a donc:

$$ n_r(a'-c)=n_i(a-c)$$

Toujours dans le cadre de l'approximation des petits angles, on peut confondre la tangente des angles $a$, $a'$ et $c$ avec les angles eux-mêmes et confondre les points $H$ et $S$. On a alors:

\begin{align*} a &= \tan(a) = \frac{HP}{AH} = \frac{HP}{AS} = \frac{HP}{-p}\\ a' &= \tan(a') = \frac{HP}{A'H} = \frac{HP}{A'S} = \frac{HP}{-p'}\\ c &= \tan(c) = \frac{HP}{CH} = \frac{HP}{CS} = \frac{HP}{-R}\\ \end{align*}

En remplaçant dans la relation de Snell-Descartes, nous obtenons:

$$\frac{n_r}{p'}-\frac{n_i}{p}=\frac{n_r-n_i}{R}=\Phi$$

Cette relation peut également se démontrer pour le dioptre divergent en gardant les mêmes conventions algébriques sur les signes. La quantité $\Phi$ s'appelle la vergence du dioptre et s'exprime en dioptrie, unité qui est homogène à des $m^{-1}$. La vergence est positive pour un dioptre convergent et négative pour un dioptre divergent.

On remarque qu'un dioptre est stigmatique de façon approchée: la position du point $A'$ est indépendante du point $P$, et donc est indépendante du rayon choisi. Cela n'est évidemment valable que dans le cadre de l'approximation de Gauss (rayons peu inclinés sur l'axe optique, angles faibles). Dans l'absolu, un dioptre sphérique n'est pas stigmatique (il existe cependant deux points sur l'axe optique, appelé "points de Weierstrass", qui vérifie la condition de stigmatisme parfait).

Foyers d'un dioptre sphérique

Un dioptre sphérique possède deux points remarquables placés sur l'axe principal, les foyers.

Il y a deux foyers, généralement notés $F$ et $F'$, connus respectivement sous le nom de foyer objet et foyer image.

On peut facilement trouver la position des foyers image et objet en utilisant la relation de conjugaison. Pour trouver la position du foyer objet, on considère que l'image est repoussée à l'infini et que p' tend donc vers l'infini, ce qui nous donne:

$$ \frac{-n_i}{f}=\frac{n_r-n_i}{R}\ \mathrm{soit}\ f=\frac{-n_i R}{n_r-n_i}=\frac{-n_i}{\Phi}$$

Pour un dioptre convergent, la distance $f=SF$ est négative, donc le foyer objet est à gauche du sommet du dioptre.

Pour le foyer image, nous avons:

$$ \frac{n_r}{f'}=\frac{n_r-n_i}{R}\ \mathrm{soit}\ f'=\frac{n_r R}{n_r-n_i}=\frac{n_r}{\Phi}$$

Pour un dioptre convergent, la distance $f'=SF'$ est donc négative, et le foyer image est à droite du sommet.

On remarquera également que les foyers ne sont pas symétriques par rapport au sommet du dioptre.

Notons enfin qu'il est possible de réécrire la relation de conjugaison en utilisant les grandeurs $f$ et $f'$, pour obtenir :

Construction de l'image d'un objet

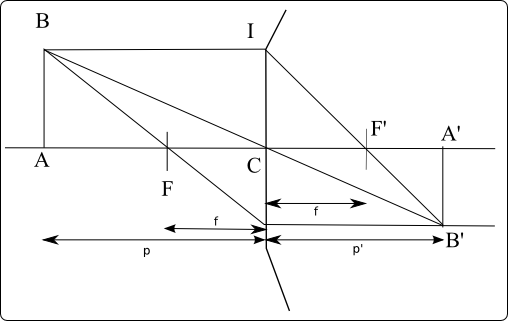
Nous nous intéressons ici à la construction de l'image de l'objet $AB$ à travers le dioptre de sommet $S$, de centre $C$ et de foyers $F$ et $F'$. Construire le point $A'$ ne pose aucun problème (il suffit d'appliquer la formule de conjugaison). Pour construire le point $B'$, nous savons qu'il existe trois rayons passant par le point $B$ qui ont un cheminement particulier. Il s'agit:

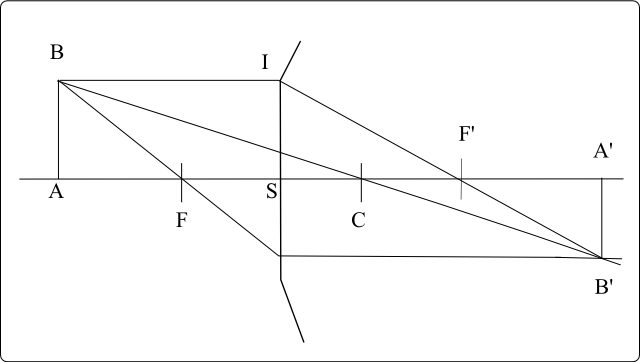
L'intersection des trois rayons se fait au point $B'$, image du point $B$.

Grandissement transverse

On appelle grandissement transverse le rapport: $$\gamma=\frac{A'B'}{AB}$$

Le rayon est paraxial, et il est donc légitime de considérer que la distance $SI$ est égale à la distance $AB$ (en toute rigueur la surface $SI$ est courbe). D'autre part, les triangles $F'IS$ et $F'A'B'$ sont homothétiques. Donc:

$$ \gamma = \frac{A'B'}{AB}= \frac{A'B'}{SI}=\frac{F'A'}{F'S}=\frac{F'S+SA'}{F'S}= \frac{-f'+p'}{-f'}=1-\frac{p'}{f'} $$

En utilisant la relation de conjugaison du dioptre, on peut réécrire le grandissement transverse de plusieurs façons:

$$ \gamma=\frac{A'B'}{AB}=1-\frac{p'}{f'}=\frac{n_i p'}{n_r p}=\frac{n_i}{n_i+p\Phi} $$

Pour une valeur donnée de $n_i$ et une vergence $\Phi$ fixée, le grandissement transverse varie suivant la fonction $$f(x)= \frac{n_i}{n_i + \Phi x}$$ On remarquera que le grandissement transverse est infini lorsque $x= - \Phi / n_i$, c'est à dire lorsque l'objet est positionné au foyer objet.

Les lentilles minces

Cas général

Une lentille est un corps homogène d'indice n limité par deux dioptres sphériques (on considère le dioptre plan comme un dioptre sphérique de rayon de courbure infini). On considèrera par la suite par soucis de simplicité que les milieux extérieurs à la lentille sont identiques et d'indice égal à 1 (l'air). Les valeurs définissant complètement une lentille sont l'indice n du milieu, la distance $S1S2$ entre les sommets des dioptres, ainsi que les rayons de courbure $r_1=S1C1$ et $r_2=S2C2$ (qui sont des valeurs algébriques).

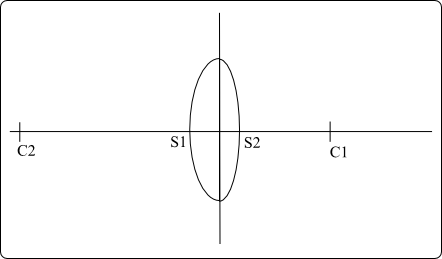
L'exemple représenté sur la figure ci-dessus est une lentille dite biconvexe, avec $r_1 \gt 0$ et $r_2\lt 0$.

L'approximation des lentilles minces

Une lentille est dite mince lorsque la distance entre les sommets est petite devant la différence des rayons de courbure:

$$ S1S2 \ll |r_1-r_2| $$

Dans ce cas, on confond les points $S1$ et $S2$ en un même point $S$.

Relation de conjugaison pour une lentille mince

La relation de conjugaison pour une lentille mince s'obtient aisément en considérant qu'il s'agit de la succession de deux dioptres de sommets confondus. On construit tout d'abord l'image Av (qui est une image virtuelle) du point A par le dioptre 1, puis l'image A' de Av par le dioptre 2. Les relations de conjugaison des dioptres nous donnent:

\begin{align*} \frac{1}{p_v}-\frac{1}{p}&=\frac{n-1}{r_1}\\ \frac{1}{p'}-\frac{1}{p_v}&=\frac{1-n}{r_2} \end{align*}

En les combinant, on obtient:

$$ \frac{1}{p'}-\frac{1}{p}=(n-1)(\frac{1}{r_1}-\frac{1}{r_2})=\Phi $$

$\Phi$ représente la vergence de la lentille. Elle est positive pour une lentille convergente, et négative pour une lentille divergente.

Foyers d'une lentille mince

La définition des foyers pour une lentille est équivalente à la définition pour les dioptres sphériques. On obtient la distance focale objet $f$ en faisant tendre $p'$ vers l'infini soit:

$$ -\frac{1}{f}=(n-1)(\frac{1}{r_1}-\frac{1}{r_2})=\Phi\ \mathrm{soit}\ f=-\frac{1}{\Phi} $$

De la même façon, la distance focale image f' est obtenue en faisant tendre p vers l'infini:

$$ -\frac{1}{f'}=(n-1)(\frac{1}{r_1}-\frac{1}{r_2})=\Phi\ \mathrm{soit}\ f'=\frac{1}{\Phi} $$

On remarque que les foyers image et objet sont symétriques par rapport au centre de la lentille puisque $f = -f'$.

Il est maintenant possible de réécrire la relation de conjugaison en introduisant les distances focales. On a alors:

Construction de l'image d'un objet

Comme pour le dioptre, nous nous intéressons ici à la construction de l'image de l'objet $AB$ à travers la lentille mince de sommet $S$ et de foyers $F$ et $F'$. Construire le point A' ne pose aucun problème (il suffit d'appliquer la formule de conjugaison). Pour construire le point $B'$, nous savons qu'il existe trois rayons passant par le point B qui ont un cheminement particulier. Il s'agit:

L'intersection des trois rayons se fait au point $B'$, image du point $B$.

Grandissement transverse pour une lentille mince

La définition du grandissement transverse reste le rapport:

$$\gamma=\frac{A'B'}{AB}$$

On peut très aisément le calculer de deux façons:

Si l'on remplace p' par sa valeur en utilisant la relation de conjugaison, on obtient:

$$\gamma=\frac{A'B'}{AB}=\frac{p'}{p}=\frac{\frac{p f}{f-p}}{p}=\frac{f}{f-p}$$

Applications de l'optique géométrique à la photographie

Qualités d'un système optique

Un système optique n'est jamais parfait. Il présente des défauts: aberration sphérique, aberration chromatique, coma, astigmatisme, courbure de champ, distorsion, etc...

Aberration chromatique

L'indice de réfraction dépend en général de la longueur d'onde dans la majorité des matériaux. On observe alors q'un rayon lumineux se disperse en fonction de la longueur d'onde de ses composants. On appelle ce phénomène l'aberration chromatique.

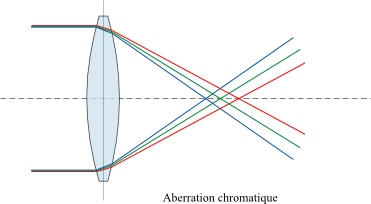
Le français Louis-Augustin Cauchy fut le premier a proposé une loi expérimentale donnant la variation de l'indice de réfraction en fonction de la longueur d'onde. Aujourd'hui la loi la plus utilisée est la loi de Sellmeier qui s'écrit sous la forme:

$$ n(\lambda) =\sqrt{1+B_1\frac{\lambda^2}{\lambda^2-C_1}+B_2\frac{\lambda^2}{\lambda^2-C_2}+B_3\frac{\lambda^2}{\lambda^2-C_3}} $$

Le nombre d'Abbe est fréquemment utilisé pour mesurer la dispersion optique d'un verre. Il se calcule par la formule suivante avec $n_d=n(589.2)$, $n_f=n(486.1)$ et $n_c=n(656.3)$:

$$V_d=\frac{n_d-1}{n_f-n_c}$$

On classe en général les verres en deux catégories, les crowns qui ont un nombre d'Abbe au dessus de 50 et un indice de réfraction relativement faible (autour de 1.5), et les flints qui ont un nombre d'Abbe inférieur à 50 et un indice de réfraction plus élevé (typiquement autour de 1.7). verre).
Un crown serait par exemple le N-PK52A de la société Schott, avec un indice de réfraction à 589nm de 1.497 et un nombre d'Abbe de 81.61, alors qu'un verre de flint serait le N-SF66 avec un indice de réfraction à 589nm de 1.92286 et un nombre d'Abbe de 20.88.

Pour construire un système achromatique, on associe en général un élément convergent et un élément divergent, l'un en verre de Flint et l'autre en verre de Crown.

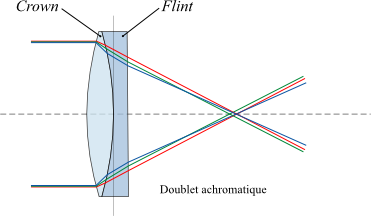
Pour réaliser un système achromatique de longueur focale f, on utilise deux lentille (une de Flint et une de Crown) de longueur focale $f_1$ et $f_2$, et l'on a la classique formule:

$$\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}$$

Si nous voulons que la focale soit la même pour les deux longueurs d'ondes extrêmes du spectre, il nous faut écrire la condition:

$$\frac{1}{f(\lambda_c)}=\frac{1}{f(\lambda_f)}$$

Soit:

$$\frac{1}{f_1(\lambda_c)}+\frac{1}{f_2(\lambda_c)}= \frac{1}{f_1(\lambda_f)}+\frac{1}{f_2(\lambda_f)}$$

Nous savons (voir plus haut) que la longueur focale ne dépend que de l'indice de réfraction et des rayons de courbure (constants) des lentilles. La formule devient donc:

$$ K_1(n_1(\lambda_c)-1)+K_2(n_2(\lambda_c)-1)=K_1(n_1(\lambda_f)-1)+K_2(n_2(\lambda_f)-1) $$

En factorisant:

$$ K_1\left(n_1(\lambda_f)-n_1(\lambda_c)\right)+K_2\left(n_2(\lambda_f)-n_2(\lambda_c)\right)=0 $$

En utilisant les nombres d'Abbe $V_1$ et $V_2$, puis en notant $n_1$ et $n_2$ les indices de réfractions pour les lentilles 1 et 2 à 589nm, nous obtenons:

$$ K_1\frac{n_1-1}{V_1}+K_2\frac{n_2-1}{V_2}=0 $$

En notant $f_1$ et $f_2$ les distances focales des lentilles 1 et 2 à 589nm, nous obtenons maintenant:

$$ \frac{1}{f_1 V_1}+\frac{1}{f_2 V_2}=0 $$

En réduisant au même dénominateur et en simplifiant, nous tombons sur la condition d'Abbe :

$$ f_1 V_1+f_2 V_2=0


La condition d'Abbe garantit que pour les longueurs d'onde "extrêmes" du spectre (486.1nm et 656.3nm) la distance focale du doublet sera exactement égale à $f$. Entre ces deux longueurs d'onde, la distance focale varie peu, mais n'est pas exactement égale à $f$.

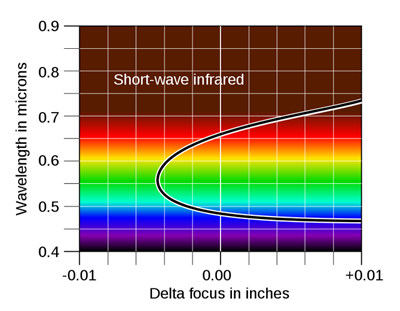
Les meilleurs objectifs modernes sont souvent apochromatiques. Il s'agit de lentilles fabriquées à partir à partir de verres ayant des propriétés particulières, comme des fluoro-crowns et des flints anormaux. Avec ces objectifs, la distance focale du doublet est exactement égale à f non pas pour deux mais pour trois longueurs d'onde (en général, une à chaque extrémité et une au centre; l'exemple ci-dessous concerne une lentille utilisée en astronomie, donc optimisée pour l'infra-rouge). Ces objectifs sont aussi corrigés de l'aberration sphérique et de la coma dont nous parlerons plus tard.

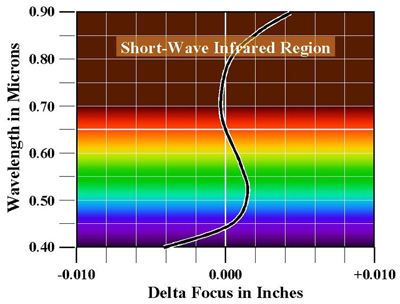
Enfin, certains objectifs trés haut de gamme, les superachromats, sont parfaitement corrigés non pas pour trois mais pour quatre longueurs d'onde (par exemple le télé-superachromat T*2.8/300 fabriqué par Zeiss pour les Hasselblad série 500). On peut voir ci-dessous l'exemple d'un objectif de ce type utilisé en astronomie.

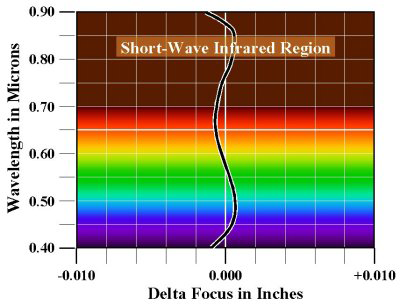
Les trois schémas ci-dessus ont été créées par Mike I. Jones, et placés dans le domaine public.

Notons pour terminer qu'il existe d'autres solutions pour réduire les aberrations chromatiques, comme l'utilisation d'éléments diffractifs, solutions utilisées par exemple par Canon sur certains de ces objectifs récentes (70/300 4.5-5.6 DO par exemple).

Stigmatisme

Le stigmatisme (qui vient du grec stigma signifiant point) est une propriété importante. Rappelons qu'un système est parfaitement stigmatique lorsque tout rayon issu d'un point A passe par un point unique image A'.

Ressources en ligne

Deux autres excellentes présentations dont je ne parviens plus à retrouver l'origine (l'auteur peut me contacter):

Retour à la page d'accueil.

Le téléchargement ou la reproduction des documents et photographies présents sur ce site sont autorisés à condition que leur origine soit explicitement mentionnée et que leur utilisation se limite à des fins non commerciales, notamment de recherche, d'éducation et d'enseignement.
Tous droits réservés.

Dernière modification: 09:14, 20/03/2024