
La polarisation
Introduction
Nous avons vu dans le chapitre consacré à l'électromagnétisme qu'une onde lumineuse peut être assimilée à une onde plane en ce qui concerne sa propagation. Les vecteurs k (définissant la direction de propagation), E (vecteur du champ électrique) et B (vecteur du champ magnétique) forment en tout point un trièdre orthogonal. L'évolution de l'onde est entièrement décrite par les équations de Maxwell, et la composante tangentielle du champ électrique et la composante normale du champ magnétique sont continues lors d'un changement de milieu.
Onde lumineuse monochromatique cohérente
Le champ magnétique et le champ électrique obéissent aux lois suivantes: $$ \begin{align*} E(r,t) &= E_0(r) e^{j(\omega t - k_0 L(r))}\\ B(r,t) &= B_0(r) e^{j(\omega t - k_0 L(r))}\\ \end{align*} $$
On voit ci-dessous l'exemple de la propagation d'une onde électromagnétique à polarisation plane. Le champ électrique E reste en permanence dans le plan "vertical", er son amplitude évolue de façon sinusoïdale, alors que le champ magnétique se trouve dans le plan orthogonal au champ électrique et au sens de propagation et évolue également de façon sinusoïdale.
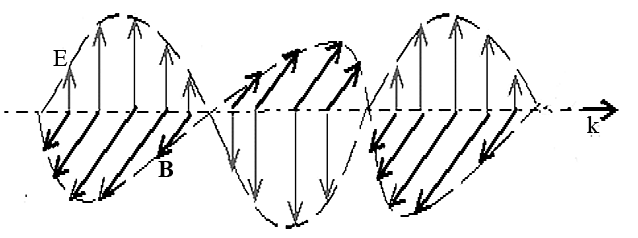
Dans le cas d'une polarisation circulaire, le champ magnétique et le champ électrique "tournent" autour de la direction de propagation de l'onde, tout en restant en permanence orthogonaux à celle-ci et orthogonaux entre eux. Le schéma suivant (extrait de wikimedia) montre la représentation 3D d'une onde polarisée circulairement.

Les ondes acoustiques ne possèdent pas de polarisation car ce sont des ondes dites "longitudinales": l'ondulation se produit suivant la direction de déplacement.
La perception de la polarisation
Certains animaux sont sensibles à la polarisation de la lumière. C'est le cas des abeilles, mais peut-être aussi des pigeons, et de certains poulpes ou calamars.
L'être humain est faiblement sensible à la polarisation de la lumière. La macula de l'oeil possède des pigments qui ont des propriétés dichroïques: cela signifie qu'ils absorbent différemment la lumière suivant sa polarisation. D'autre part, la couche extérieure de certains cones semblent avoir des propriétés biréfringentes: les rayons qui la traversent sont déviés de façon différente suivant la polarisation de la lumière.
La composition de ces deux phénomènes crée une figure connue sous le nom de "pinceaux d'Haidinger" que l'on peut voir en représentation simulée sur la figure suivante:

Pour arriver à voir cette figure, il existe plusieurs méthodes, mais la plus simple est de regarder une zone blanche sur un écran LCD (les écrans LCD sont équipés de filtres polarisants). En fixant bien attentivement l'écran et en penchant légèrement la tête, la figure finit par apparaitre; en ce qui me concerne, elle ressemble à deux tâches jaunes, comme si l'écran était légèrement sale. La figure est loin d'être aussi visible que celle représentée sur l'écran.
La polarisation de la lumière est cependant une propriété importante, même si elle est apparemment invisible. Certaines lunettes de soleil sont équipées de filtre polarisant qui élimine toutes les ondes lumineuses (ou toutes les composantes de ces ondes) qui ont le champ électrique dans un plan donné.
Sur une lumière qui est déjà complètement polarisée, comme
celle émise par un écran LCD, il est possible en utilisant ces
lunettes polarisantes, d'obscurcir complètement l'écran. Vous pouvez
obtenir le même effet avec un filtre polarisant.
On peut voir ci-dessous l'effet d'un filtre polarisant utilisé sur un
écran LCD, suivant que l'on filtre totalement l'onde ou qu'on ne la
filtre pas du tout.


En lumière naturelle, une onde n'est ni monochromatique, ni cohérente. En effet, les ondes émises par la majorité des sources lumineuses comportent plusieurs longueurs d'ondes, mais possèdent également plusieurs polarisations différentes. Ces sources n'émettent pas en fait une onde, mais plusieurs paquets d'ondes, qui ont chacun leurs propriétés spécifiques.
Ainsi, les lunettes polarisantes vont éliminer en moyenne la moitié de l'intensité lumineuse. D'autre part, ces lunettes ont une caractéristique particulièrement intéressante: elles éliminent tout particulièrement la composante de la lumière qui est réfléchie par une surface plane, comme la surface d'un lac, un miroir, ou une vitre.
Si vous utilisez ces lunettes et que vous regardez la surface d'un lac, vous verrez nettement mieux le fond de l'eau, car les reflexions parasites en surface sont éliminés. Pour le ciel, la couleur sera un bleu plus profond, car les réflexions engendrées par les molécules en suspension seront également éliminées.
Il faut cependant savoir que ce phénomène est surtout sensible pour un angle particulier (appelé angle de Brewster) qui est proche de 45 degrés, et dépend des indices de réfraction des deux matériaux qui composent le dioptre.
Nous allons maintenant expliquer comment ce phénomène physique se produit.
Traversée d'un dioptre plan par une onde électromagnétique
On commence par décomposer le champ électrique de l'onde incidente en deux composantes, l'une dans le plan d'incidence (si vous voulez, le plan de votre écran sur ce schéma) et l'autre orthogonale à ce plan.
Lorsque seule la deuxième composante est présente, on parle d'onde électrique transverse, généralement notée TE. Lorsque seule la première composante est présente, on parle d'onde magnétique transverse (on la note alors TM). Cette dernière appellation est justifiée par le fait que le champ magnétique est toujours orthogonal au champ électrique, et si le champ électrique est dans le champ d'incidence, alors le champ magnétique lui est orthogonal.
Ce qui nous intéresse, c'est de savoir comment chacun de ces types d'onde se comporte lorsqu'elle rencontre la surface du dioptre. Une onde générale pouvant s'écrire comme la combinaison de ces deux types d'onde, cela nous permettra de connaitre le comportement général d'une onde quelconque.
Le calcul est relativement complexe, et on peut le trouver sur cet excellent document.
En ce qui nous concerne, nous allons nous contenter de regarder le résultat de ce calcul, et l'interpréter.
Onde électrique transverse
Les coefficients donnant les amplitudes des ondes réflechi et transmises dans le cas d'une onde incidente électrique transverse (TE) pure sont donnés par les équations suivantes: $$ \begin{align*} r_{te}=\frac{n_1\cos(\theta_1)-n_2\cos(\theta_2)}{n_1\cos(\theta_1)+n_2\cos(\theta_2)}\\ t_{te}=\frac{2n_1\cos(\theta_1)}{n_1\cos(\theta_1)+n_2\cos(\theta_2)} \end{align*} $$
Onde magnétique transverse
Les coefficients donnant les amplitudes des ondes réflechie et transmise dans le cas d'une onde incidente magnétique transverse (TM) pure sont donnés par les équations suivantes: $$ \begin{align*} r_{tm}=\frac{n_2\cos(\theta_1)-n_1\cos(\theta_2)}{n_2\cos(\theta_1)+n_1\cos(\theta_2)}\\ t_{tm}=\frac{2n_1\cos(\theta_1)}{n_2\cos(\theta_1)+n_1\cos(\theta_2)} \end{align*} $$ Nous allons nous intéresser plus en détail au coefficient de l'onde réflechi. On voit qu'il peut être égal à 0 si $$ n_2\cos(\theta_1)=n_1\cos(\theta_2) $$ Comme d'autre part on a, suivant la loi de Snell-Descartes: $$ n_1\sin(\theta_1)=n_2\sin(\theta_2) $$ En résolvant le système d'équation, on obtient: $$ \theta_1=\arctan(\frac{n_2}{n_1}) $$
$\theta_1$ est l'angle de Brewster. Lorsque l'on regarde la surface d'une vitre ou de l'eau suivant l'angle de Brewster, la seule onde réfléchie visible est l'onde électrique transverse, la composante magnétique transverse est elle totalement éliminée par la réflexion.
Pour ce qui concerne, par exemple la surface de l'eau, l'angle de Brewster vaut environ 54 degrés. Si l'on utilise des lunettes polarisées ou un filtre polarisant à cet incidence, et que l'on filtre la seule composante restante (l'électrique transverse) toutes les réflexions sont éliminées, et le fond de l'eau devient alors beaucoup plus visible.
On observe le même phénomène pour la réflexion sur une vitre. On voit ci-dessous l'exemple d'une photographie d'une réflexion sur une vitre. A gauche, on n'utilise pas de filtre polarisant. La réflexion est totalement visible, et on voit parfaitement un élément de placard (la barre verticale est un croisillon de la fenêtre); à droite, le filtre polarisant a fait totalement disparaitre la réflexion et on peut voir à travers la vitre les barreaux d'une chaise blanche à l'extérieur (la photo a été prise de nuit, l'extérieur est donc dans l'ombre).


On remarquera également, à titre indicatif, que la mise au point est faite sur l'objet virtuel qui correspond à la réflexion dans la vitre, et que le croisillon est donc flou, puisqu'il est "plus près" que l'objet virtuel.
Polarisant circulaire
Examinons maintenant un dernier problème, celui des polarisants pour appareil photo.
Nous avons jusque là décrit des filtres polarisants (lunettes) qui
éliminent une composante de la lumière qui les traverse. Bien
entendu, la composante qui est éliminée dépend de l'orientation du
filtre. C'est le même principe que celui des filtres polarisants
d'appareil photo. La rotation du filtre permet de choisir quelle
composante de la lumière sera éliminée. Dit plus savamment, on choisit
le vecteur de la base sur lequel on va projeter le vecteur champ
électrique; en tournant le polarisant, on fait tourner ce vecteur.
Cependant, cette rotation n'a rien à voir avec le nom de
polarisant circulaire. En fait, pour un appareil photographique non
autofocus et non reflex, on pourrait utiliser des verres de lunette de
soleil polarisants comme filtre, cela marcherait très bien.
Malheureusement, le mécanisme d'un reflex autofocus pose un petit problème: la lumière, pour atteindre le système autofocus, est renvoyé par un miroir. Or, le miroir se comporte comme il se doit, c'est à dire qu'il polarise la lumière qu'il réfléchit, surtout lorsqu'elle arrive suivant l'angle de Brewster. Or les miroirs autofocus sont généralement orientés à 45 degrés, une valeur proche de l'angle de Brewster. Donc, si nous n'avons pas de chance, le polariseur placé devant la lentille va éliminer une composante de l'onde. Si on a éliminé la composante électrique transverse (au sens du miroir), le miroir va lui éliminer la composante magnétique transverse et il ne restera plus de lumière du tout, et l'autofocus ne fonctionnera plus.
Les filtres polarisants d'appareil photo sont donc plus complexes. Ils
sont généralement composés de deux filtres successifs. Le premier est
un polarisant linéaire traditionnel. Le second est généralement ce que
l'on appelle un filtre "quart de tour". Il s'agit d'un filtre qui fait
tourner d'un quart de tour la polarisation d'une partie des paquets
d'onde qui le traverse, créant ainsi une onde qui a une polarisation
qui n'est plus plane. Après réflexion sur le miroir, il restera donc
suffisamment de lumière pour faire fonctionner l'autofocus.
C'est ce que l'on appelle un polarisant circulaire.

Quelques exemples d'utilisation de filtre polarisant
On peut voir ci-dessous un exemple classique d'utilisation d'un
polarisant circulaire pour photographier un lac de montagne
dominé par un petit pic. Sur la photo de gauche (sans polarisant) le
reflet du pic dans le lac est parfaitement visible. Sur la photo de
droite (avec polarisant), le reflet du pic a quasiment disparu, et le
lac apparait avec un bleu profond. On constate également une
modification dans la couleur du ciel, puisque le polarisant élimine
une partie de la réflexion atmosphérique, et permet d'obtenir là-aussi
un bleu plus profond.
Le but n'est pas ici de dire que la photographie avec polarisant est
systématiquement meilleure que celle faite sans polarisant. On peut
d'ailleurs préférer la photo de gauche (la réflexion du pic dans le
lac donne un effet tout à fait intéressant). Le polarisant circulaire
est simplement un outil supplémentaire à la disposition du
photographe, à utiliser à bon escient.


Le téléchargement ou la reproduction des documents et photographies
présents sur ce site sont autorisés à condition que leur origine soit
explicitement mentionnée et que leur utilisation
se limite à des fins non commerciales, notamment de recherche,
d'éducation et d'enseignement.
Tous droits réservés.
Dernière modification: 21:15, 08/03/2024