headlogo2

La diffraction

Introduction

L'autre élément susceptible de rendre vos photos floues (en dehors de la profondeur de champ discuté ici ) est la diffraction.

La diffraction est un phénomène inévitable lié à la nature ondulatoire de la lumière. Malheureusement, la comprendre est un petit peu plus compliqué que comprendre les problèmes de profondeur de champ, car il faut faire appel à quelques intégrales et, dans le cas qui nous intéresse des diaphragmes ronds, aux fonctions dites de Bessel.

Il est cependant fondamental de bien comprendre cette notion. C'est en particulier la diffraction qui pose une limite théorique à la densité maximale de photosites sur un capteur numérique.

Nous avons déjà examiné les problèmes d'interférence d'ondes dans le cadre général des ondes planes et sphériques. Les résultats que nous avons énoncés à cette occasion restent valables dans le cadre des ondes lumineuses, à quelques petites différences près. Le lecteur est donc invité à relire ces deux pages avant de poursuivre.

Principe de Huyghens-Fresnel

Le principe de Huyghens-Fresnel a été énoncé par Huyghens en 1678 puis raffiné par Fresnel en 1818. Une première démonstration sous de "bonnes hypothèses" a été faite par Kirchhof en 1882, et un traitement plus exhaustif a été réalise par Sommerfeld en 1896.

L'expression du principe de Huyghens-Fresnel est simple: pour une onde incidente sur une ouverture, chaque élément de l'ouverture peut être vue à son tour comme une source ponctuelle émettant une onde sphérique dont l'intensité dépend de la surface de l'élément. La résultante de toutes ces ondes ponctuelles va nous donner l'onde diffractée. On devine donc qu'en passant à la limite de la taille d'un élément de surface, on va passer d'une somme à une intégrale double portant sur toute la surface.

Huyghens a énoncé ce principe à partir de résultats expérimentaux.

L'expérience des deux trous

Cette expérience permet de démontrer à la fois le principe de Huyghens-Fresnel et la nature ondulatoire de la lumière. Une source de lumière est placée derrière un écran noir, percé de deux trous, qui sont supposés être "ponctuels" (physiquement très petits). Ces deux trous vont agir comme des sources de lumière indépendantes qui ont cependant la même phase. A une distance d, on place un écran blanc et on observe la figure d'interférence résultante. Ce dispositif expérimental assure que les rayons sont cohérents: ils partagent la même fréquence et la même phase.

Dans ce premier paragraphe, nous allons faire un certain nombre de simplifications permettant de présenter une version simple de cette expérience. Dans le paragraphe suivant, nous examinerons le cas de la diffraction avec une seule fente, mais en faisant moins de simplifications.

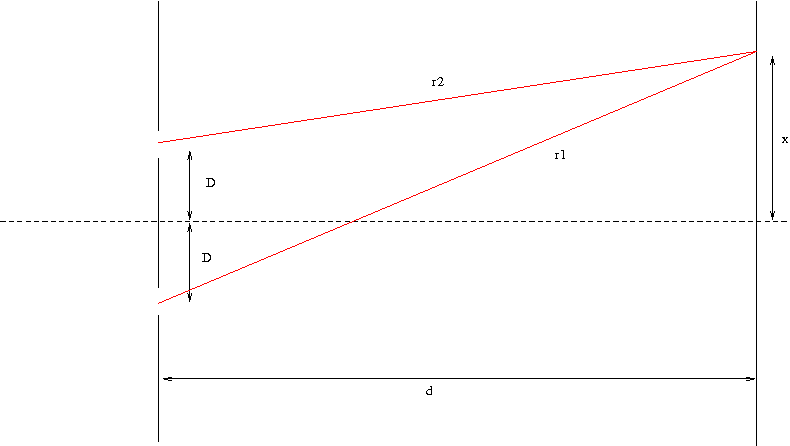
Les conditions de l'expérience sont les suivantes: $D$ est du même ordre que $\lambda$ (la longueur d'onde de la lumière). $D$ et $x$ sont petits devant $d$ ($x$ est environ dix fois plus petit que $d$).

Nous utiliserons ces ordres de grandeur pour faire les développements limités nécessaires dans les formules suivantes.

Calculons $r_1$: $$ r_1=\sqrt{d^2+(x+D)^2} $$ En faisant un développement limité, nous obtenons: $$ r_1=d\left(1+\frac{1}{2}\left(\frac{x+D}{d}\right)^2\right) $$

$r_2$ est obtenu en effectuant un calcul symétrique: $$ r_2=d\left(1+\frac{1}{2}\left(\frac{x-D}{d}\right)^2\right) $$

La différence $r_1-r_2$ vaut donc en ne conservant évidmment que les termes du premier ordre: $$ r_1-r_2= 2 \frac{D}{d} x $$

L'interférence entre les deux ondes s'obtient en calculant la somme: $$ f(x,t)=A\cos\left(2 \pi (f t - \frac{r_1}{\lambda})\right)+ A\cos\left(2 \pi (f t - \frac{r_2}{\lambda})\right) $$ En transformant la somme des cosinus en produit, nous obtenons: $$ f(x,t) = 2A \cos\left(2 \pi \frac{r_1-r_2}{2 \lambda}\right) \cos\left(2 \pi \left(f t-\frac{r_1+r_2}{2 \lambda}\right)\right) $$ Remplaçons $r_1-r_2$ par la valeur trouvée précédemment: $$ f(x,t) = 2A \cos\left(2 \pi \frac{D}{d\lambda}x\right) \cos\left(2 \pi \left(f t-\frac{r_1+r_2}{2 \lambda}\right)\right) $$

L'oeil est sensible seulement à l'énergie moyenne de cette onde. Nous avons dans la section consacrée aux ondes planes que cette énergie vaut dans le cas de cette onde: $$ E(x)=2A^2 \cos^2\left(2 \pi \frac{D}{d\lambda}x\right) $$

La figure suivante montre la variation d'intensité de la lumière sur l'écran avec $d=1m$ et $D/\lambda=20$

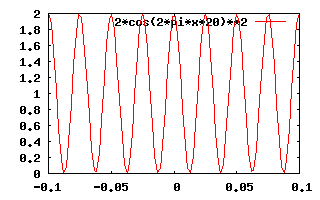
L'écran montre donc une alternance de bandes blanches et noires dont l'intensité varie avec le carré du cosinus

La première expérience de ce type fut réalisé par Thomas Young en 1803. Il présenta à la Royal Society le schéma suivant:

Young n'utilisa pas des "trous", mais plutôt des fentes verticales très fines. Cette expérience est resté célèbre sous le nom d'expérience de Young. En 1818, Augustin-Jean Fresnel posa les bases théoriques de la diffraction de la lumière et, de la nature ondulatoire de la lumière.

Diffraction à l'infini avec une fente

Dans la suite de ce paragraphe, nous utiliserons la notation complexe qui simplifie grandement les calculs en remplaçant les cosinus par des exponentielles complexes dont la partie réelle correspond au cosinus utilisé habituellement (cette notation a déjà été introduite dans le chapitre consacré à l'électromagnétisme. L'énergie d'une onde peut être obtenu en multipliant la valeur complexe par son conjugué. Nous écrirons donc: $$ I(r,t) = e^{j 2 \pi \left(f t - \frac{r}{\lambda}\right)}= e^{j (\omega t - \phi)}= e^{j \omega t} e^{ - j\phi} $$ avec $\omega = 2 \pi f$ et $\phi = 2 \pi \frac{r}{\lambda}$

$e^{-j \phi}$ est appelé l'amplitude complexe de l'onde. En écrivant $I(r,t)$ en notation complexe, on sépare la partie spatiale (l'amplitude complexe) de la partie dépendant du temps. Cette dernière ne nous intéresse pas ici, car nous ne cherchons à calculer que des énergies, qui sont des moyennes.

Nous allons maintenant calculer la figure de diffraction d'une fente sur un écran placé à l'infini. Pour observer la figure d'interférence, on utilise une lentille convergente et on place l'écran au point focal de la lentille. Sans diffraction, un seul point devrait apparaître sur l'écran en $F'$. La diffraction modifie profondément le résultat.

Les conditions sus-mentionnées sont connues sous le nom de conditions de Fraunhoffer. Le calcul des figures de diffraction avec des écrans proches de l'objet diffractant s'appelle diffraction de Fresnel, et fait appel à des techniques mathématiques beaucoup plus complexes.

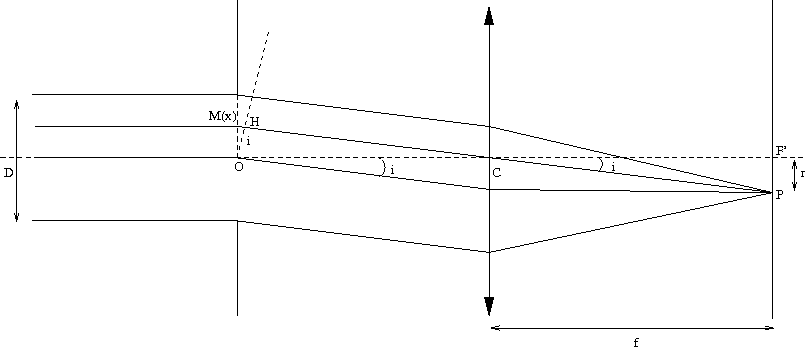
Il nous faut tout d'abord calculer la différence de phase entre le rayon passant par $M(x)$ et le rayon passant par $O$. La différence de chemin optique est la distance $HM(x)=x \tan(i)= x i$ pour un angle $i$ petit. La différence de phase est donc: $$ \phi = 2 \pi \frac{x}{\lambda} i $$ L'amplitude complexe totale est obtenue en intégrant sur chaque partie élémentaire: $$ I(i) = \int_{-D/2}^{D/2}{A e^{ j 2 \pi i \frac{x}{\lambda}}\, d\!x} $$ Posons $ u = 2 \pi \frac{i}{\lambda}$. Nous avons: $$ I(i) = \int_{-D/2}^{D/2}{A e^{ j x u}\, d\!x}= A\left[\frac{e^{ j x u}}{ju}\right]_{-D/2}^{D/2}= A\left(\frac{e^{ j u D/2}-e^{ j u (-D/2)}}{ju}\right) $$ En utilisant les identités: \begin{align*} \sin(x)&=\frac{e^{jx}-e^{-jx}}{2j}\\ \mathrm{sinc}(x)&=\frac{\sin(x)}{x} \end{align*} nous avons: $$ I(i)= A \frac{2}{u}\sin\left(\frac{u D}{2}\right) = A D \frac{\sin\left(\frac{u D}{2}\right)}{\frac{u D}{2}} = A D\ \mathrm{sinc}\left(\frac{u D}{2}\right) = I_0\ \mathrm{sinc}\left(\frac{u D}{2}\right) $$ avec $I_0=A D$. Remplaçons $u$ par sa valeur: $$ I(i) = I_0\ \mathrm{sinc}\left(\pi \frac{D}{\lambda} i \right) $$

L'intensité réelle est égale à l'intensité complexe multipliée par son conjugué. L'intensité complexe étant déjà réelle, cela revient à l'élever au carré: $$ I(i) = I_0^2\ \mathrm{sinc}^2\left(\pi \frac{D}{\lambda} i \right) $$

L'intensité est maximale pour $i=0$ et sa valeur en ce point est $I_0=(A D)^2$. Nous allons tracer la fonction $\frac{E(i)}{I_0^2}$

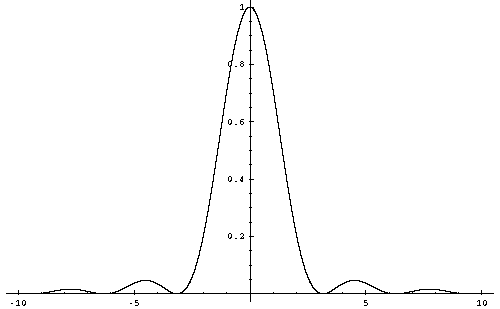
Le premier zéro de la fonction est obtenu pour $$i=\frac{\lambda}{D}$$ La taille de la tâche de diffraction sur l'écran est: $$ r= f \tan(i) = f i = \lambda \frac{f}{D} = \lambda O $$ où O est l'ouverture.

Diffraction à l'infini avec un diaphragme circulaire

La diffraction avec un diaphragme circulaire se calcule exactement de la même façon, en intégrant non plus sur une fente, mais sur le disque entier (intégrale double).

Le calcul est compliqué, et fait apparaître la fonction de Bessel du premier ordre $J_1(x)$: $$ E(i)=I_0^2 \left(2 \frac{J_1\left(\pi \frac{D}{\lambda} i\right)}{\pi \frac{D}{\lambda} i } \right)^2 $$ Si nous traçons la fonction $(2 \frac{J_1(x)}{x})^2$, nous obtenons:

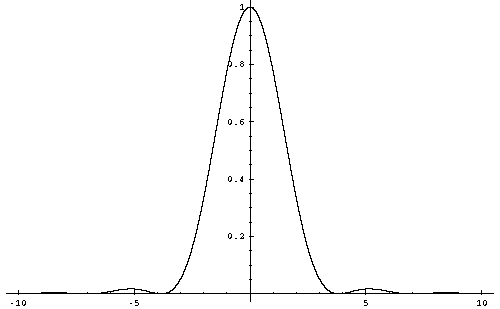
Le premier zéro de cette fonction est obtenu pour $x=3.80$, soit $i = 1.22 \frac{\lambda}{D}$
La tache de diffraction (connue également sous le nom de tâche d'Airy) a un rayon de: $$ r = f \tan(i) = f i = 1.22 \lambda \frac{f}{D} = 1.22 \lambda O $$

Le rayon de la tâche de diffraction dépend donc seulement de la longueur d'onde $\lambda$ et de l'ouverture $O$.

Applications numériques pour la photographie

Pour une longueur d'onde $400 \lt \lambda \lt 800$ nanomètres, la taille de la tache de diffraction en micron vaut environ: $$ \frac{O}{2} \lt r \lt O $$

Sur la plupart des reflex numériques, la taille d'une photodiode est de l'ordre de 5 microns. La diffraction devient donc visible pour une ouverture entre 5 et 10 suivant la longueur d'onde. Elle sera plus visible dans les rouges que dans les bleus. Avec des photodiodes plus petites (~2 microns) comme celles utilisées sur les smartphones, la diffraction va apparaître très tôt, entre 2 et 4. Les capteurs de petite taille des smartphones sont extrêmement sensibles à la diffraction, et augmenter le nombre de photodiodes sans modifier la taille du capteur ne fera qu'amplifier le phénomène.

On peut fortement douter de la nécessité de la course aux pixels sur des capteurs de cette taille.

Il faut cependant mettre un petit bémol; la plupart des appareils utilisent des mosaïques Bayer qui alternent capteur vert et capteur rouge ou bleu. Le cercle de confusion peut venir couvrir deux capteurs adjacents, mais cela ne modifie pas autant la résolution que si chaque pixel captait les trois longueurs d'onde comme sur les capteurs Foveon.

Ce dont il faut se souvenir

Ressources en ligne:

How to read MTF curves

Retour à la page d'accueil.

Le téléchargement ou la reproduction des documents et photographies présents sur ce site sont autorisés à condition que leur origine soit explicitement mentionnée et que leur utilisation se limite à des fins non commerciales, notamment de recherche, d'éducation et d'enseignement.
Tous droits réservés.

Dernière modification: 09:23, 21/03/2024